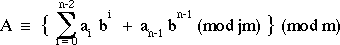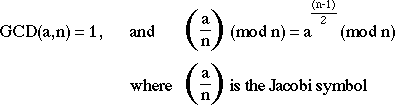Number Theory and Public Key Cryptography
Introduction to Number Theory
Modular Arithmetic
- modular arithmetic is 'clock arithmetic'
- a congruence a = b mod n says when divided by n
that a and b have the same remainder
- 100 = 34 mod 11
- usually have 0<=b<=n-1
- -12mod7 = -5mod7 = 2mod7 = 9mod7
- b is called the residue of a mod n
- can do arithmetic with integers modulo n with all results between 0 and n
- addition
- a+b mod n
- subtraction
- a-b mod n = a+(-b) mod n
- multiplication
- a.b mod n
- derived from repeated addition
- can get a.b=0 where neither a,b=0
- division
- a/b mod n
- is multiplication by inverse of b: a/b = a.b-1 mod n
- if n is prime b-1 mod n exists s.t
b.b-1 = 1 mod n
- eg 2.3=1 mod 5 hence 4/2=4.3=2 mod 5
- integers modulo n with addition and multiplication form a commutative ring
with the laws of
- Associativity
- (a+b)+c = a+(b+c) mod n
- Commutativity
- a+b = b+a mod n
- Distributivity
- (a+b).c = (a.c)+(b.c) mod n
- also can chose whether to do an operation and then reduce modulo n, or
reduce then do the operation, since reduction is a homomorphism from the ring
of integers to the ring of integers modulo n
- a+/-b mod n = [a mod n +/- b mod n] mod n
- (the above laws also hold for multiplication)
- if n is constrained to be a prime number p then this forms a
Galois Field modulo p denoted GF(p) and all the normal laws
associated with integer arithmetic work
Exponentiation in GF(p)
- many encryption algorithms use exponentiation - raising a number
a (base) to some power b (exponent) mod p
- exponentiation is basically repeated multiplication, which take s
O(n) multiples for a number n
- a better method is the square and multiply algorithm[1]
let base = a, result =1
for each bit ei (LSB to MSB) of exponent
if ei=0 then
square base mod p
if ei=1 then
multiply result by base mod p
square base mod p (except for MSB)
required ae is result
- only takes O(log2 n) multiples for a number
n
see Sebbery p9 Fig2.1 + example
Discrete Logarithms in GF(p)
- the inverse problem to exponentiation is that of finding the discrete
logarithm of a number modulo p
- find x where ax = b mod p
Seberry examples p10
- whilst exponentiation is relatively easy, finding discrete logarithms is
generally a hard problem, with no easy way
- in this problem, we can show that if p is prime, then there
always exists an a such that there is always a discrete logarithm for
any b!=0
- successive powers of a "generate" the group mod p
- such an a is called a primitive root and these are also
relatively hard to find
Greatest Common Divisor
- the greatest common divisor (a,b) of a and b
is the largest number that divides evenly into both a and b
- Euclid's Algorithm is used to find the Greatest Common Divisor
(GCD) of two numbers a and n, a<n
- use fact if a and b have divisor d so does
a-b, a-2b
GCD (a,n) is given by:
let g0=n
g1=a
gi+1 = gi-1 mod gi
when gi=0 then (a,n) = gi-1
eg
find (56,98)
g0=98
g1=56
g2 = 98 mod 56 = 42
g3 = 56 mod 42 = 14
g4 = 42 mod 14 = 0
hence
(56,98)=14
see Seberry Fig 2.2 p11 GCD alg [2]
Inverses and Euclid's Extended GCD Routine
- unlike normal integer arithmetic, sometimes a number in modular arithmetic
has a unique inverse
- a-1 is inverse of a mod n if
a.a-1 = 1 mod n
- where a,x in {0,n-1}
- eg 3.7 = 1 mod 10
- if (a,n)=1 then the inverse always exists
- can extend Euclid's Algorithm to find Inverse by keeping
track of gi = ui.n + vi.a
- Extended Euclid's (or Binary GCD) Algorithm to find
Inverse of a number a mod n (where (a,n)=1) is:
Inverse(a,n) is given by:
g0=n u0=1 v0=0
g1=a u1=0 v1=1
let
y = gi-1 div gi
gi+1 = gi-1 - y.gi = gi-1 mod gi
ui+1 = ui-1 - y.ui
vi+1 = vi-1 - y.vi
when gi=0 then Inverse(a,n) = vi-1
Example
eg: want to find Inverse(3,460):
i y g u v
0 - 460 1 0
1 - 3 0 1
2 153 1 1 -153
3 3 0 -3 460
hence Inverse(3,460) = -153 = 307 mod 460
see Seberry Fig 2.3 p14 Inverse alg [3]
Euler Totient Function [[phi]](n)
- if consider arithmetic modulo n, then a reduced set of residues is
a subset of the complete set of residues modulo n which are relatively prime to
n
- eg for n=10,
- the complete set of residues is {0,1,2,3,4,5,6,7,8,9}
- the reduced set of residues is {1,3,7,9}
- the number of elements in the reduced set of residues is called the
Euler Totient function [[phi]](n)
- there is no single formula for [[phi]](n) but for various cases count how
many elements are excluded[4]:
p (p prime) [[phi]](p) =p-1
pr (p prime) [[phi]](p) =pr-1(p-1)
p.q (p,q prime) [[phi]](p.q) =(p-1)(q-1)
see Seberry Table 2.1 p13
- several important results based on [[phi]](n) are:
- Theorem (Euler's Generalization)
- let gcd(a,n)=1 then
- a[[phi]](n) mod n = 1
- Fermat's Theorem
- let p be a prime and gcd(a,p)=1 then
- ap-1 mod p = 1
- Algorithms to find Inverses a-1 mod n
- search 1,...,n-1 until an a-1 is found with
a.a-1 mod n
- if [[phi]](n) is known, then from Euler's Generalization
- a-1 = a[[phi]](n)-1 mod n
- otherwise use Extended Euclid's algorithm for inverse
Computing with Polynomials in GF(qn)
- have seen arithmetic modulo a prime number GF(p)
- also can do arithmetic modulo q over polynomials of degree
n, which also form a Galois Field GF(qn)
- its elements are polynomials of degree (n-1) or lower
-
a(x)=an-1xn-1+an-2xn-2+...+a1x+a0
- have residues for polynomials just as for integers
- p(x)=q(x)d(x)+r(x)
- and this is unique if deg[r(x)]<deg[d(x)]
- if r(x)=0, then d(x) divides p(x), or is a factor of p(x)
- addition in GF(qn) just involves summing equivalent terms in
the polynomial modulo q (XOR if q=2)
-
a(x)+b(x)=(an-1+bn-1)xn-1+...+(a1+b1)x+(a0+b0)
Multiplication with Polynomials in GF(qn)
- multiplication in GF(qn) involves [5]
- multiplying the two polynomials together (cf longhand multiplication; here
use shifts & XORs if q=2)
- then finding the residue modulo a given irreducible polynomial of
degree n
- an irreducible polynomial d(x) is a 'prime' polynomial, it has no
polynomial divisors other than itself and 1
- modulo reduction of p(x) consists of finding some r(x) st:
p(x)=q(x)d(x)+r(x)
- nb. in GF(2n) with d(x)=x3+x+1 can do
simply by replacing x3 with x+1
- eg in GF(23) there are 8 elements:
- 0, 1, x, x+1, x2, x2+1, x2+x,
x2+x+1
- with irreducible polynomial d(x)=x3+x+1* arithmetic
in this field can be summarised as:
Seberry Table 2.3 p20
- can adapt GCD, Inverse, and CRT algorithms for GF(qn)
- [[phi]](p(x)) = 2n-1 since every poly except 0 is
relatively prime to p(x)
- arithmetic in GF(qn) can be much faster than integer
arithmetic, especially if the irreducible polynomial is carefully chosen
- eg a fast implementation of GF(2127) exists
- has both advantages and disadvantages for cryptography, calculations are
faster, as are methods for breaking
-
Complexity Theory - A Potted Intro
- Complexity theory - study of how hard a problem is to solve in general
- allows classification of types of problems
- some problems intrinsically harder than others, eg
- multiplying numbers O(n^(2))
- multiplying matrices O(n^(2)(2n-1))
- solving crossword O(26^(n))
- recognizing primes O(n^(log log n))
- deal with worst case complexity
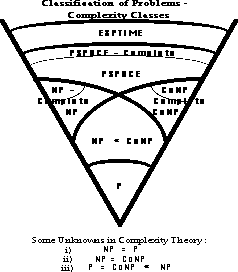
Complexity Theory - Some Terminolgy
- an instance of a problem is a particular case of a general problem
- the input length of a problem is the number n of symbols
used to characterize a particular instance of it
- the order of a function f(n) - is some O(g(n)) of
some function g(n) s.t.
- f(n)<=c.|g(n)|, for all n>=0, for some c
- a polynomial time algorithm (P) is one which solves any
instance of a particular problem in a length of time O(p(n)), where p is some
polynomial on input length
- an exponential time algorithm (E) - is one whose solution
time is not so bounded
- a non-deterministic polynomial time algorithm (NP) - is one
for which any guess at the solution of an instance of the problem may be
checked for validity in polynomial time
- NP-complete problems - are a subclass of NP problems for which it
is known that if any such problem has a polynomial time solution, then all
NP problems have polynomial solutions. These are thus the hardest NP
problems
- Co-NP problems - are the complements of NP problems, to
prove a guess at a solution of a Co-NP problem may well require an exhaustive
search of the solution space
Public-Key Ciphers
- traditional secret key cryptography uses a single key shared by
both sender and receiver
- if this key is disclosed communications are compromised
- also does not protect sender from receiver forging a message &
claiming is sent by sender, parties are equal
- public-key (or two-key) cryptography involves the use
of two keys:
- a public-key, which may be known by anybody, and can be used to
encrypt messages, and verify signatures
- a private-key, known only to the recipient, used to decrypt
messages, and sign (create) signatures
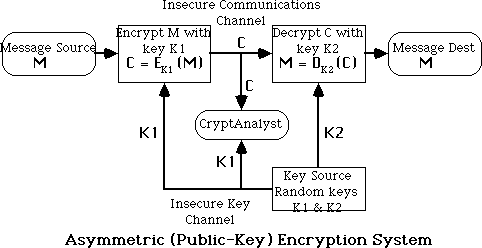
- the public-key is easily computed from the private key and other
information about the cipher (a polynomial time (P-time) problem)
- however, knowing the public-key and public description of the cipher, it
is still computationally infeasible to compute the private key (an NP-time
problem)
- thus the public-key may be distributed to anyone wishing to communicate
securly with its owner (although secure distribution of the public-key is a
non-trivial problem - the key distribution problem)
- have three important classes of public-key algorithms:
- Public-Key Distribution Schemes (PKDS) - where the scheme is used
to securly exchange a single piece of information (whose value depends on the
two parties, but cannot be set).
- This value is normally used as a session key for a private-key scheme
- Signature Schemes - used to create a digital signature only, where
the private-key signs (create) signatures, and the public-key verifies
signatures
- Public Key Schemes (PKS) - used for encryption, where the
public-key encrypts messages, and the private-key decrypts messages.
- Any public-key scheme can be used as a PKDS, just by selecting a message
which is the required session key
- Many public-key schemes are also signature schemes (provided encryption
& decryption can be done in either order)
Digital Signatures and Signature Schemes
- where the private-key signs (create) signatures, and the public-key
verifies signatures
- only the owner can create the digital signature, hence it can be used to
verify who created a message
- generally don't sign the whole message (doubling the size of information
exchanged), but just a digest or hash of the message,
- a hash function takes the message, and produces a fixed size
(typically 64 to 512 bits) value dependent on the message
- it must be hard to create another message with the same hash value
(otherwise some forgeries are possible)
- developing good hash functions is another non-trivial problem
Diffie-Hellman Public-Key Distribution Scheme
- first public-key type scheme proposed was a PKDS by Diffie & Hellman
in 1976:
W Diffie, M E Hellman, "New directions in Cryptography", IEEE Trans.
Information Theory, IT-22, pp644-654, Nov 1976
- an excellent overview of cryptography at this time is:
W Diffie, M E Hellman, "Privacy and Authentication: An Introduction to
Cryptography", Proc. of the IEEE, Vol 67 No 3, pp 397-427, Mar 1979
- it is a public-key distribution scheme
- it cannot be used to exchange an arbitrary message
- only a key, whose value depends on the participants (and their private and
public key information)
- is based on exponentiation in a finite (Galois) field, either over
integers modulo a prime, or a polynomial field
- nb exponentiation takes O((log n)3) operations
- its security relies on the difficulty of computing logarithms in these
fields
- nb discrete logarithms takes O(e log n log log n) operations
- Diffie-Hellman PKDS works as follows:
- two people A & B, who wish to exchange some key over an insecure
communications channel can:
- select a large prime p (~200 digit), and
- [[alpha]] a primitive element mod p
- A has a secret number xA
- B has a secret number xB
- A and B compute yA and yB respectively, which
are then made public
- yA = [[alpha]]xA mod p
yB = [[alpha]]xB mod p
- the key is then calculated as
- KAB = [[alpha]]xA.xB mod p
- = yAxB mod p (which
B can compute)
- = yBxA mod p (which
A can compute)
- and may then be used in a private-key cipher to secure communications
between A and B
- nb: if the same two people subsequently wish to communicate, they will
have the same key as before, unless they change their public-key
(usually not often)
RSA Public-Key Cryptosystem
- best known and widely regarded as most practical public-key scheme was
proposed by Rivest, Shamir & Adleman in 1977:
R L Rivest, A Shamir, L Adleman, "On Digital Signatures and Public Key
Cryptosystems", Communications of the ACM, vol 21 no 2, pp120-126, Feb 1978
- it is a public-key scheme which may be used for encrypting messages,
exchanging keys, and creating digital signatures
- is based on exponentiation in a finite (Galois) field over integers modulo
a prime
- nb exponentiation takes O((log n)3) operations
- its security relies on the difficulty of calculating factors of large
numbers
- nb factorization takes O(e log n log log n) operations
- (same as for discrete logarithms)
- the algorithm is patented in North America (although algorithms cannot be
patented elsewhere in the world)
- this is a source of legal difficulties in using the scheme
- RSA is a public key encryption algorithm based on exponentiation using
modular arithmetic
- to use the scheme, first generate keys:
- Key-Generation by each user consists of:
- selecting two large primes at random (~100 digit), p, q
- calculating the system modulus R=p.q p, q primes
- selecting at random the encryption key e,
- e < R, gcd(e, F(R)) = 1
- solving the congruence to find the decryption key d,
- e.d [[equivalence]] 1 mod [[phi]](R) 0
<= d <= R
- publishing the public encryption key: K1={e,R}
- securing the private decryption key: K2={d,p,q}
- Encryption of a message M to obtain ciphertext C is:
- C = Me mod R 0 <= d <=
R
- Decryption of a ciphertext C to recover the message M is:
- M = Cd = Me.d =
M1+n.[[phi]](R) = M mod R
- the RSA system is based on the following result:
if R = pq where p, q are distinct large primes then
X [[phi]](R) = 1 mod R
for all x not divisible by p or q
and [[Phi]](R) = (p-1)(q-1)
RSA Example
- usually the encryption key e is a small number, which must be relatively
prime to [[phi]](R) (ie GCD(e, [[phi]](R)) = 1)
- typically e may be the same for all users (provided certain precautions
are taken), 3 is suggested
- the decryption key d is found by solving the congruence:
e.d [[equivalence]] 1 mod [[phi]](R), 0 <= d <= R,
- an extended Euclid's GCD or Binary GCD calculation is done to do this.
given e=3, R=11*47=517, [[phi]](R)=10*46=460
then d=Inverse(3,460) by Euclid's alg:
i y g u v
0 - 460 1 0
1 - 3 0 1
2 153 1 1 -153
3 3 0 -3 460
ie: d = -153, or 307 mod 517
- a sample RSA encryption/decryption calculation is:
M = 26
C = 263 mod 517 = 515
M = 515307 mod 517 = 26
Security of RSA
- The security of the RSA scheme rests on the difficulty of factoring the
modulus of the scheme R
- best known factorization algorithm (Brent-Pollard) takes:
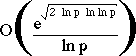
operations on number R whose largest prime factor is p
Decimal Digits in R #Bit Operations to Factor R
20 7200
40 3.11e+06
60 4.63e+08
80 3.72e+10
100 1.97e+12
120 7.69e+13
140 2.35e+15
160 5.92e+16
180 1.26e+18
200 2.36e+19
- This leads to R having a length of 200 digits (or 600 bits) given that
modern computers perform 1-100 MIPS the above can be divided by 106
to get a time in seconds
- nb: currently 1e+14 operations is regarded as a limit for computational
feasability and there are 3e+13 usec/year
- but most (all!!) computers can't directly handle numbers larger than
32-bits (64-bits on the very newest)
- hence need to use multiple precision arithmetic libraries to handle
numbers this large
Multi-Precision Arithmetic
- involves libraries of functions that work on multiword (multiple
precision) numbers
- classic references are in Knuth vol 2 - "Seminumerical Algorithms"
- multiplication digit by digit
- do exponentiation using square and multiply[6]
- are a number of well known multiple precision libraries available - so
don't reinvent the wheel!!!!
- can use special tricks when doing modulo arithmetic, especially with the
modulo reductions
Faster Modulo Reduction
* Chivers (1984) noted a fast way of performing modulo reductions whilst doing
multi-precision arithmetic calcs
Given an integer A of n characters (a0, ... , an-1) of
base b
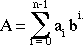 then
then
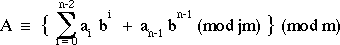
ie: this implies that the MSD of a number can be removed and its remainder mod
m added to the remaining digits will result in a number that is congruent mod m
to the original.
* Chivers algorithm for reducing a number is thus:
1. Construct an array R = (bd, 2.bd, ... ,
(b-1).bd)(mod m)
2. FOR i = n-1 to d do
WHILE A[i] != 0 do
j = A[i];
A[i] = 0;
A = A + bi-d.R[j];
END WHILE
END FOR
where A[i] is the ith character of number A
R[j] is the jth integer residue from the array R
n is the number of symbols in A
d is the number of symbols in the modulus
Speeding up RSA - Alternate Multiplication Techniques
- conventional multiplication takes O(n2) bit operations, faster
techniques include:
- the Schonhage-Strassen Integer Multiplication Algorithm:
- breaks each integer into blocks, and uses them as coefficients of a
polynomial
- evaluates these polynomials at suitable points, & multiplies the
resultant values
- interpolates these values to form the coefficients of the product
polynomial
- combines the coefficients to form the product of the original integer
- the Discrete Fourier Transform, and the Convolution Theorem are used to
speed up the interpolation stage
- can multiply in O(n log n) bit operations
- the use of specialized hardware because:
- conventional arithmetic units don't scale up, due to carry propogation
delays
- so can use serial-parallel carry-save, or delayed carry-save techniques
with O(n) gates to multiply in O(n) bit operations,
- or can use parallel-parallel techniques with O(n2) gates to
multiply in O(log n) bit operations
RSA and the Chinese Remainder Theorem
- a significant improvement in decryption speed for RSA can be obtained by
using the Chinese Remainder theorem to work modulo p and q respectively
- since p,q are only half the size of R=p.q and thus the arithmetic is much
faster
- CRT is used in RSA by creating two equations from the decryption
calculation:
M = Cd mod R
as
follows:
M1 = M mod p = (C mod p)d mod (p-1)
M2 = M mod q = (C mod q)d mod (q-1)
then
the pair of equations
M = M1 mod p M = M2 mod q
has
a unique solution by the CRT, given by:
M = [((M2 +q - M1)u mod q] p + M1
where
p.u mod q = 1
Primality Testing and RSA
- The first stage of key-generation for RSA involves finding two large
primes p, q
- Because of the size of numbers used, must find primes by trial and error
- Modern primality tests utilize properties of primes eg:
- an-1 = 1 mod n where GCD(a,n)=1
- all primes numbers 'n' will satisfy this equation
- some composite numbers will also satisfy the equation, and are called
pseudo-primes.
- Most modern tests guess at a prime number 'n', then take a large number
(eg 100) of numbers 'a', and apply this test to each. If it fails the number is
composite, otherwise it is is probably prime.
- There are a number of stronger tests which will accept fewer composites as
prime than the above test. eg:
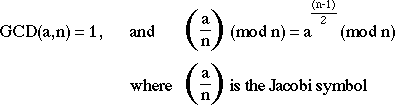
RSA Implementation in Practice
- Software implementations
- generally perform at 1-10 bits/second on block sizes of 256-512 bits
- two main types of implementations:
- - on micros as part of a key exchange mechanism in a hybrid scheme
- - on larger machines as components of a secure mail system
- Harware Implementations
- generally perform 100-10000 bits/sec on blocks sizes of 256-512 bits
- all known implementations are large bit length conventional ALU
units
El Gamal
- a variant of the Diffie-Hellman key distribution scheme, allowing secure
exchange of messages
- published in 1985 by ElGamal in
T. ElGamal, "A Public Key Cryptosystem and a Signature Scheme Based on
Discrete Logarithms", IEEE Trans. Information Theory, vol IT-31(4), pp469-472,
July 1985.
- like Diffie-Hellman its security depends on the difficulty of factoring
logarithms
- Key Generation
- select a large prime p (~200 digit), and
- [[alpha]] a primitive element mod p
- A has a secret number xA
- B has a secret number xB
- A and B compute yA and yB respectively,
which are then made public
- yA = [[alpha]]xA mod p
- yB = [[alpha]]xB mod p
- to encrypt a message M into ciphertext C,
- selects a random number k, 0 <= k <= p-1
- computes the message key K
- computes the ciphertext pair: C = {c1,c2}
- C1 = [[alpha]]k mod p
C2 = K.M mod p
- to decrypt the message
- extracts the message key K
- K = C1xB mod p =
[[alpha]]k.xB mod p
- extracts M by solving for M in the following equation:
Other Public-Key Schemes
- a number of other public-key schemes have been proposed, some of the
better known being:
- Knapsack based schemes
- McEleice's Error Correcting Code based schems
- ALL of these schemes have been broken
- the only currently known secure public key schemes are those based on
exponentiation
(all of which are patented in North America)
- it has proved to be very very difficult to develop secure public key
schemes
- this in part is why they have not been adopted faster, as their
theorectical advantages might have suggested
[1] examples: 7^5 -> a=7, e={101}
[2] more examples: GCD(84,60)=12; GCD(323,238)=17;
GCD(323,299)=1;
[3]more examples: Inv(299,323)=148 show trace of g=u.n+v.a
[4] show examples: eg [[phi]] of 3, 3.3, 3.5
[5] example: a=x^2+1, find a^2 mod (x^3+x+1)=x^2+x+1 showing
modulo reduction process
[6] follow with examples of multiple precision arithmetic
[CSC Info]
Lawrie.Brown@adfa.oz.au / 24-Apr-96
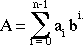 then
then


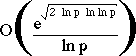
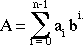 then
then