Classical Cryptography

Introduction to Cryptography

cryptography is the study of

secret (crypto-) writing (-graphy)

concerned with developing algorithms which may be used to:
- conceal the context of some message from all except the sender and recipient (privacy or secrecy), and/or
- verify the correctness of a message to the recipient (authentication)

form the basis of many technological solutions to computer and communications security problems

for a good overview paper see:

W Diffie, M E Hellman, "Privacy and Authentication: An Introduction to Cryptography", in Proc. IEEE, Vol 67(3) Mar 1979, pp 397-427

Basic Concepts

cryptography: the art or science encompassing the principles and methods of transforming an intelligible message into one that is unintelligible, and then retransforming that message back to its original form
plaintext: the original intelligible message
ciphertext: the transformed message
cipher: an algorithm for transforming an intelligible message into one that is unintelligible by transposition and/or substitution methods
key: some critical information used by the cipher, known only to the sender & receiver
encipher (encode): the process of converting plaintext to ciphertext using a cipher and a key
decipher (decode): the process of converting ciphertext back into plaintext using a cipher and a key
cryptanalysis: the study of principles and methods of transforming an unintelligible message back into an intelligible message without knowledge of the key. Also called codebreaking
cryptology: both cryptography and cryptanalysis
code: an algorithm for transforming an intelligible message into an unintelligible one using a code-book

Concepts

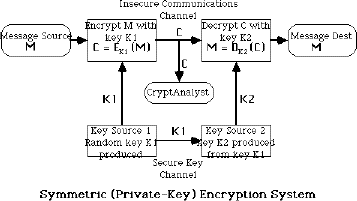
Encryption C = E_(K)(P)

Decryption P = E_(K)^(-1)(C)

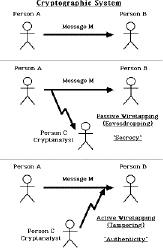
E_(K) is chosen from a family of transformations known as a cryptographic system.

The parameter that selects the individual transformation is called the key K, selected from a keyspace K

More formally a cryptographic system is a single parameter family of invertible transformations

E_(K) ; K in K : P -> C

with the inverse algorithm E_(K)^(-1) ; K in K : C -> P

such that the inverse is unique

Usually assume the cryptographic system is public, and only the key is secret information

Private-Key Encryption Algorithms

a private-key (or secret-key, or single-key) encryption algorithm is one where the sender and the recipient share a common, or closely related, key

all traditional encryption algorithms are private-key

overview of a private-key encryption system and attacker

Cryptanalytic Attacks

have several different types of attacks

ciphertext only

only have access to some enciphered messages
use statistical attacks only

known plaintext

know (or strongly suspect) some plaintext-ciphertext pairs
use this knowledge in attacking cipher

chosen plaintext

can select plaintext and obtain corresponding ciphertext
use knowledge of algorithm structure in attack

chosen plaintext-ciphertext

can select plaintext and obtain corresponding ciphertext, or select ciphertext and obtain plaintext
allows further knowledge of algorithm structure to be used

Unconditional and Computational Security

two fundamentally different ways ciphers may be secure

unconditional security
- no matter how much computer power is available, the cipher cannot be broken
computational security
- given limited computing resources (eg time needed for calculations is greater than age of universe), the cipher cannot be broken

A Brief History of Cryptography

Ancient Ciphers

have a history of at least 4000 years
ancient Egyptians enciphered some of their hieroglyphic writing on monuments

ancient Hebrews enciphered certain words in the scriptures
2000 years ago Julius Ceasar used a simple substitution cipher, now known as the Caesar cipher
Roger Bacon described several methods in 1200s
Geoffrey Chaucer included several ciphers in his works
Leon Alberti devised a cipher wheel, and described the principles of frequency analysis in the 1460s
Blaise de Vigenère published a book on cryptology in 1585, & described the polyalphabetic substitution cipher
increasing use, esp in diplomacy & war over centuries

Machine Ciphers

Jefferson cylinder, developed in 1790s, comprised 36 disks, each with a random alphabet, order of disks was key, message was set, then another row became cipher

Wheatstone disc, originally invented by Wadsworth in 1817, but developed by Wheatstone in 1860's, comprised two concentric wheels used to generate a polyalphabetic cipher

Enigma Rotor machine, one of a very important class of cipher machines, heavily used during 2nd world war, comprised a series of rotor wheels with internal cross-connections, providing a substitution using a continuosly changing alphabet

Classical Cryptographic Techniques

have two basic components of classical ciphers: substitution and transposition
in substitution ciphers letters are replaced by other letters
in transposition ciphers the letters are arranged in a different order
these ciphers may be:
monoalphabetic - only one substitution/ transposition is used, or
polyalphabetic - where several substitutions/ transpositions are used
several such ciphers may be concatentated together to form a product cipher

Caesar Cipher - a monoalphabetic cipher

replace each letter of message by a letter a fixed distance away eg use the 3rd letter on
reputedly used by Julius Caesar

eg.

	L FDPH L VDZ L FRQTXHUHG
	I CAME I SAW I CONQUERED

ie mapping is

	ABCDEFGHIJKLMNOPQRSTUVWXYZ
	DEFGHIJKLMNOPQRSTUVWXYZABC

can describe this cipher as:

Encryption E_(k) : i -> i + k mod 26

Decryption D_(k) : i -> i - k mod 26

Cryptanalysis of the Caesar Cipher

only have 26 possible ciphers
could simply try each in turn - exhaustive key search

				GDUCUGQFRMPCNJYACJCRRCPQ
				HEVDVHRGSNQDOKZBDKDSSDQR
	Plain	-	IFWEWISHTOREPLACELETTERS
				JGXFXJTIUPSFQMBDFMFUUFST
				KHYGYKUJVQTGRNCEGNGVVGTU
	Cipher -	LIZHZLVKWRUHSODFHOHWWHUV
				MJAIAMWLXSVITPEGIPIXXIVW

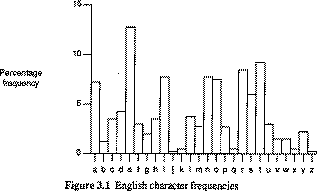
also can use letter frequency analysis

Single Letter              Double Letter             Triple Letter              
E                          TH                        THE                        
T                          HE                        AND                        
R                          IN                        TIO                        
N                          ER                        ATI                        
I                          RE                        FOR                        
O                          ON                        THA                        
A                          AN                        TER                        
S                          EN                        RES

Character Frequencies

in most languages letters are not equally common
in English e is by far the most common letter
have tables of single double & triple letter frequencies
these are different for different languages (see Appendix A in Seberry & Pieprzyk)

use these tables to compare with letter frequencies in ciphertext, since a monoalphabetic substitution does not change relative letter frequencies

[1]

do need a moderate amount of ciphertext (100+ letters)

Modular Arithmetic monoalphabetic cipher

more generally could use a more complex equation to calculate the ciphertext letter for each plaintext letter

E_(a b) : i ->a.i + b mod 26

nb a must not divide 26 (ie gcd(a,26) = 1)

otherwise cipher is not reversible eg a=2

and a=0, b=1, c=2 ... , y=24, z=25

eg E_(5 7) : i ->5.i + 7 mod 26

Cryptanalysis:

use letter frequency counts to guess a couple of possible letter mappings
- nb frequency pattern not produced just by a shift
use these mappings to solve 2 simultaneous equations to derive above parameters

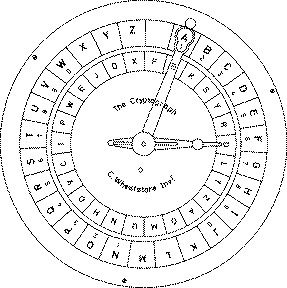
Example - Sinkov pp 34-35

Mixed Alphabets

most generally we could use an arbitrary mixed (jumbled) alphabet
each plaintext letter is given a different random ciphertext letter, hence key is 26 letters long

Plain:   ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher:  DKVQFIBJWPESCXHTMYAUOLRGZN
Plaintext:  IFWEWISHTOREPLACELETTERS
Ciphertext: WIRFRWAJUHYFTSDVFSFUUFYA

now have a total of 26! ^(~) 4 ^(x) 10^(26) keys
with so many keys, might think this is secure

!!!WRONG!!!

problem is not the number of keys, rather:

1) there is lots of statistical information in message

2) can solve the problem piece by piece

(ie can get key nearly right, and nearly get message)

(near enough MUST NOT be good enough!)

Cryptanalysis

use frequency counts to guess letter by letter
also have frequencies for digraphs & trigraphs

General Monoalphabetic

special form of mixed alphabet
use key as follows:
- write key (with repeated letters deleted)
- then write all remaining letters in columns underneath
- then read off by columns to get ciphertext equivalents

Example Seberry p66

	STARW
	BCDEF
	GHIJK
	LMNOP
	QUVXY
	Z

Plain:  ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: SBGLQZTCHMUADINVREJOXWFKPY

Plaintext:  I KNOW ONLY THAT I KNOW NOTHING
Ciphertext: H UINF NIAP OCSO H UINF INOCHIT

Polyalphabetic Substitution

in general use more than one substitution alphabet
makes cryptanalysis harder since have more alphabets to guess
and because flattens frequency distribution
(since same plaintext letter gets replaced by several ciphertext letter, depending on which alphabet is used)

Vigenère Cipher

basically multiple caesar ciphers
key is multiple letters long K = k_(1) k_(2) ... k_(d)
ith letter specifies ith alphabet to use
use each alphabet in turn, repeating from start after d letters in message

Plaintext	THISPROCESSCANALSOBEEXPRESSED
Keyword		CIPHERCIPHERCIPHERCIPHERCIPHE
Plaintext	VPXZTIQKTZWTCVPSWFDMTETIGAHLH

can use a Saint-Cyr Slide for easier encryption

based on a Vigenère Tableau


   ABCDEFGHIJKLMNOPQRSTUVWXYZ

A  ABCDEFGHIJKLMNOPQRSTUVWXYZ
B  BCDEFGHIJKLMNOPQRSTUVWXYZA
C  CDEFGHIJKLMNOPQRSTUVWXYZAB
D  DEFGHIJKLMNOPQRSTUVWXYZABC
E  EFGHIJKLMNOPQRSTUVWXYZABCD
F  FGHIJKLMNOPQRSTUVWXYZABCDE
G  GHIJKLMNOPQRSTUVWXYZABCDEF
H  HIJKLMNOPQRSTUVWXYZABCDEFG
I  IJKLMNOPQRSTUVWXYZABCDEFGH
J  JKLMNOPQRSTUVWXYZABCDEFGHI
K  KLMNOPQRSTUVWXYZABCDEFGHIJ
L  LMNOPQRSTUVWXYZABCDEFGHIJK
M  MNOPQRSTUVWXYZABCDEFGHIJKL
N  NOPQRSTUVWXYZABCDEFGHIJKLM
O  OPQRSTUVWXYZABCDEFGHIJKLMN
P  PQRSTUVWXYZABCDEFGHIJKLMNO
Q  QRSTUVWXYZABCDEFGHIJKLMNOP
R  RSTUVWXYZABCDEFGHIJKLMNOPQ
S  STUVWXYZABCDEFGHIJKLMNOPQR
T  TUVWXYZABCDEFGHIJKLMNOPQRS
U  UVWXYZABCDEFGHIJKLMNOPQRST
V  VWXYZABCDEFGHIJKLMNOPQRSTU
W  WXYZABCDEFGHIJKLMNOPQRSTUV
X  XYZABCDEFGHIJKLMNOPQRSTUVW
Y  YZABCDEFGHIJKLMNOPQRSTUVWX
Z  ZABCDEFGHIJKLMNOPQRSTUVWXY

can describe this cipher as:

given K = k_(1) k_(2) ... k_(d)

then f_(i) (a) = a + k_(i) (mod n)

Beauford Cipher

similar to Vigenère but with alphabet written backwards
can be descibed by

given K = k_(1) k_(2) ... k_(d)

then f_(i) (a) = (k_(i) - a) (mod n)

and its inverse is

f_(i) ^(-1)(a) = (k_(i) - c) (mod n)

Example - Seberry p71

Key = d
Plain:   ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher:  DCBAZYXWVUTSRQPONMLKJIHGFE

Variant-Beauford Cipher

just the inverse of the Vigenère (decrypts it)

given K = k_(1) k_(2) ... k_(d)

then f_(i) (a) = a - k_(i) (mod n)

Language Redundancy & Unicity Distance

human languages are highly redundant
- eg th lrd s m shphrd shll nt wnt
Claude Shannon derived several important results about the information content of languages in 1949
entropy of a message H(X) is related to the number of bits of information needed to encode a message X [2]
- cannot exceed log_(2)n bits for n possible messages
the rate of langauge for messages of length k denotes the average number of bits in each character

D = F(H(M),k)

rate of English is about 3.2 bits/letter
distinguish information context and redundancy
Shannon defined the unicity distance of a cipher to give a quantatative measure of:
- the security of a cipher (must not be too small)
- the amount of ciphertext N needed to break it

N = F(H(K),D)

where H(K) is entropy (amount of info) of the key,

and is D the rate of the language used (eg 3.2)

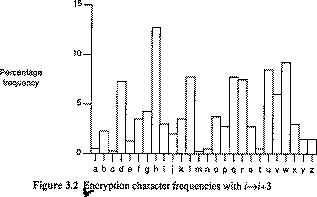
for polynomial based monoalphabetic substitution ciphers have:

N = F(H(K),D) = F(log_(2)26,3.2) = 1.5

hence only need 2 letters to break

for general monoalphabetic substitution ciphers have

N = F(H(K),D) = F(log_(2)n!,D) = F(log_(2)26!,3.2) = F(26 log_(2)F(26,e),3.2) = 27.6

hence only need 27 or 28 letters to break

for polyalphabetic substitution ciphers, if have s possible keys for each simple subs, and d keys used, then

N = F(H(K),D) = F(log_(2)s^(d),D) = F(d log_(2)26,3.2) = 1.5d

hence need 1.5 times the number of separate substitutions used letters to break the cipher

but first need to determine just how many alphabets were used
- Kasiski method
- index of coincidence

Kasiski Method

use repetitions in ciphertext to give clues as to period, looking for same plaintext an exact period apart, leading to same ciphertext

Example - Seberry p71

Plaintext:   TOBEORNOTTOBE
Key:         NOWNOWNOWNOWN
Ciphertext:  GCXRCNACPGCXR

Since repeats are 9 chars apart, guess period is 3 or 9.

Index of Coincidence

Index of Coincidence (IC) was introduced in 1920s by William Friedman
measures variation of frequencies of letters in ciphertext
- period = 1 => simple subs => variation is high, IC high
- period > 1 => poly subs => variation is reduced, IC low

see Seberry Table 3.2 p72 and Table 3.3 p74

d           IC              
1           0.0660          
2           0.0520          
3           0.0473          
4           0.0450          
5           0.0436          
6           0.0427          
7           0.0420          
8           0.0415          
9           0.0411          
10          0.0408          
11          0.0405          
12          0.0403          
13          0.0402          
14          0.0400          
15          0.0399          
...         ...             
Inf         0.0380

	Table 3.3 - Period and IC for English

first define a measure of roughness (MR) giving variation of frequencies of individual characters relative to a uniform distribution

		MR = Isu(i=o,n-1,(p_(i) - F(1,n))^(2))

where p_(i) is probability an arbitrary character in ciphertext is the ith character a_(i) in the alphabet

			 Isu(i=o,n-1,p_(i)) = 1

for English letters can derive

		MR = Isu(i=o,n-1,p_(i)^(2)) - 0.038

		MR + 0.038 = Isu(i=o,n-1,p_(i)^(2))

is prob two arbitrary letters in ciphertext are the same

can compute MR for plaintext using characteristic letter frequencies

eg MR for English is 0.028 (0.066 - 0.038)

can also compute MR for a flat distribution as 0
since probabilities and period are unknown, cannot compute MR, however can estimate from ciphertext
now the number of pairs of letters that can be chosen from ciphertext of length N is

		Bbc[(S(N,2)) = F(1,2) N (N-1)

if F_(i) is the freq of the ith letter of English in the ciphertext, then the number of pairs containing just the ith letter is

		F(F_(i)(F_(i)-1),2)		and	Isu(i=o,n-1,F_(i)) = 1

now define the Index of Coincidence (IC) as the prob that two letters at random from the ciphertext are indeed the same

	IC = 	Isu(i=o,n-1,F(F_(i)(F_(i)-1),N(N-1)))

and use the IC estimate in

		MR + 0.038 = IC

since usually use IC in crypto work, expect that

		0.038 < IC < 0.066

for a cipher of period d the expected value of the IC is

		Exp(IC) = F(1,d) F(N-d,N-1)(0.066) + Bbc[(S(d-1,d))F(N,N-1)(0.038)

and we can use these values to estimate d from the ciphertext

Example program to compute IC - Seberry Fig3.4 p74

Solving Polyalphabetic Ciphers

use Kasiski method & IC to estimate period d
then separate ciphertext into d sections, and solve each as a monoalphabetic cipher

Example - Seberry pp73-77

Krypto program

this is a program to help solve simple substitution and transposition ciphers
invoke using

krypto [file]

has the following commands available

       Command                                    Meaning                            
?                       this message.                                                
!                       execute a shell command.                                     
f [<seqlen> [n]]        print [the n most] frequent strings of length seqlen.        
g [<d> <p>]             print the frequency distribution graph of letters.           
i [<p>]                 calculate the index of coincidence of the text.              
l [<b> <B>]             list only the modified string.  [b=blklength, B=blks/line]   
p                       print current code.                                          
q                       exit.                                                        
s <ch1> <ch2>           substitute ch2 for ch1.                                      
S [-] -[gvbB] {keys}    Perform the substitution specified by the key.               
T [-] <perm>|key        Transpose text by perm or keyword. e.g. T 4,5,2,3,1          
t <n> [/regexp]         look for transpositions of period n;  [print only /regexp].  
B [-] <perm>|key        apply the specifed rectangular encryption to the text.       
b <n> [/regexp]         look for block decryptions of size n;  [print only           
                        /regexp].                                                    
u                       undo previous modification.                                  
z                       reset the code to its initial state.                         
r <file>                enter code from file.                                        
w <file>                write code to file.                                          
e                       edit code.

see man entry for more details

Transposition Ciphers

transposition or permutation ciphers hide the message contents by rearranging the order of the letters

Scytale cipher

an early Greek transposition cipher
a strip of paper was wound round a staff
message written along staff in rows, then paper removed
leaving a strip of seemingly random letters

not very secure as key was width of paper & staff

For information on lots of simple substitution and permutation ciphers see:

A. Sinkov "Elementary Cryptanalysis", New Mathematical Library, Random House, 1968* other simple transposition ciphers include:

Reverse cipher

write the message backwards

Plain:	I CAME I SAW I CONQUERED
Cipher:	DEREU QNOCI WASIE MACI

Rail Fence cipher

write message with letters on alternate rows
read off cipher row by row

Plain:	I A E S W C N U R D
         C M I A I O Q E E 
Cipher:	IAESW CNURD CMIAI OQEE

Geometric Figure

write message following one pattern and read out with another

Row Transposition ciphers

in general write message in a number of columns and then use some rule to read off from these columns
key could be a series of number being the order to: read off the cipher; or write in the plaintext


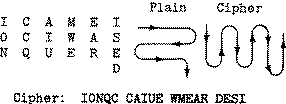
Plain:	THESIMPLESTPOSSIBLETRANSPOSITIONSXX
Key (R):      2 5 4 1 3	
Key (W):                           4 1 5 3 2 	

              T H E S I		S T I E H 	
              M P L E S		E M S L P 	
              T P O S S		S T S O P 	
              I B L E T		E I T L B 	
              R A N S P		S R P N A 	
              O S I T I		T O I I S 	
              O N S X X		X O X S N 
Cipher:	STIEH EMSLP STSOP EITLB SRPNA TOIIS XOXSN

Example - Davies p26 Fig 2.14

or can use a word, with letter order giving sequence: to write in the plaintext; or read off the cipher


Plain:	ACONVENIENTWAYTOEXPRESSTHEPERMUTATION
Key (W):      C O M P U T E R
Key (W):      1 4 3 5 8 7 2 6
 	
              A N O V I N C E
              E W T A O T N Y
              H E P R T U E M
              A O I N Z Z T Z

Cipher:       ANOVI NCEEW TAOTN YHEPR TUEMA OINZZ TZ

Example - Davies p26 Fig 2.15

key idea for row transposition ciphers is that message is in groups that have the letters reordered in each
Exercise using key sorcery (to read out) encipher:

Key(R):	sorcery => 6 3 4 1 2 5 7
laser beams can be modulated to carry more intelligence than radio waves

gives

erasb lecam snabd umole atoed ctamo ryrre elntl iicee ntgha dnria oesav w

decryption consists of:
- writing the message out in columns
- reading off the message by reordering columns
- (use T command in krypto, uses read out keys)
hint - its not a good idea to leave message in groups matching the size of your key!!!

Cryptanalysis of Row Transposition ciphers

a frequency count will show a normal language profile
hence know have letters rearranged
basic idea is to guess period, then look at all possible permutations in period, and search for common patterns (eg t command in krypto)
use lists of common pairs & triples & other features

Example - Seberry p67-8 [3]

to determine the complexity of this cipher, we can calculate its unicity distance
- given blocks of period d, there are d! keys, hence

N = F(H(K),D) = F(log_(2)d!,D) = F(d log_(2)(d/e),3.2)

Seberry Table 3.1 p69

Block (Columnar) Transposition ciphers

another group of ciphers are block (columnar) transposition ciphers where the message is written in rows, but read off by columns in order given by key (use B command in krypto)
for ease of recovery may insist matrix is filled


Key(R):       s o r c e r y        s o r c e r y
Key(R):       6 3 4 1 2 5 7        6 3 4 1 2 5 7

              l a s e r b e        l a s e r b e
              a m s c a n b        a m s c a n b
              e m o d u l a        e m o d u l a
              t e d t o c a        t e d t o c a
              r r y m o r e        r r y m o r e 
              i n t e l l i        i n t e l l i
              g e n c e t h        g e n c e t h
              a n r a d i o        a n r a d i o
              w a v e s            w a v e s q r

giving ciphertext (by reading off cols 4, 5, 2, 3, 6, 1, 7)

ecdtm ecaer auool edsam merne nasso dytnr vbnlc rltiq laetr igawe baaei hor

decryption consists of:
- calculating how many rows there are (by dividing message length by key length)
- then write out message down columns in order given by key

Example - Sinkov p148

exercise - Sinkov p148 #74

Sinkov p148

Cryptanalysis of Block Transposition ciphers

again know must be a transposition, and guess is perhaps a block transposition
guess size of matrix by looking at factors of message length, and write out by columns
then look for ways of reordering pairs of columns to give common pairs or triples (very much trial & error)
(nb use b command in krypto to try possibilities)

Example - Sinkov p 149-151

Nihilist ciphers

a more complex transposition cipher using both row and column transpositions is the nihilist cipher
write message in rows in order controlled by the key (as for a row cipher)
then read off by rows, but in order controlled by the key, this time written down the side
uses a period of size the square of the key length

Plaintext:    NOWISTHETIMEFORALLGOODMEN

Key (W):             L E M O N
                     2 1 3 5 4
              L 2    O N W S I
              E 1    H T E I T
              M 3    E M F R O
              0 5    L A L O G
              N 4    D O M N E

Nihilist Cipher:     HTEIT ONWSI EMFRO DOMNE LALOG

Diagonal Cipher:     ONHET WSEML DAFII TRLOM OOGNE

Example - Davis Fig2.16 p27

attacking this cipher depends on column and row rearrangement, with much trial and error
for more complexity can vary readout algorithm
- diagonal cipher reads out on fwd diag (/) in alternate directions (up diag, down diag etc), ie a zig-zag read out

Product ciphers

can see that in general ciphers based on just substitutions or just transpositions are not secure
what about using several ciphers in order
- two substitutions are really only one more complex substitution
- two transpositions are really only one more complex transposition
- but a substitution followed by a transposition makes a new much harder cipher
product ciphers consist substitution-transposition combinations chained together
in general are far too hard to do by hand, however one famous product cipher, the 'ADFGVX' cipher was used in WW1 (see Kahn pp339-350)
instead there use had to wait for the invention of the cipher machine, particularly the rotor machines (eg Enigma, Hagalin) mentioned briefly earlier

ADFGVX Product Cipher

named since only letters ADFGVX are used
chosen since have very distinct morse codes
uses a fixed substitution table to map each plaintext letter to a letter pair (row-col index)
then uses a keyed block transposition

	
Substitution Table

\\    A     D     F     G     V     X     
A     K     Z     W     R     1     F     
D     9     B     6     C     L     5     
F     Q     7     J     P     G     X     
G     E     V     Y     3     A     N     
V     8     O     D     H     0     2     
X     U     4     I     S     T     M


	Plaintext:	PRODUCTCIPHERS
	
	Intermediate Text:
				FG AG VD VF XA DG XV
				DG XF FG VG GA AG XG

Keyed Block Columnlar Transposition Matrix

D     E     U     T     S     C     H        Key                     
2     3     7     6     5     1     4        Sorted Order            
F     G     A     G     V     D     V                                
F     X     A     D     G     X     V                                
D     G     X     F     F     G     V                                
G     G     A     A     G     X     G


	Ciphertext:	DXGX FFDG GXGG VVVG VGFG CDFA AAXA

[1] follow w Seberry App A-1 p1; Sinkov Ex 9 & 10 p 20
[2] see Seberry Section 2.4 for detailed derivations
[3]follow with example Seberry p68

[CSC Info]

Lawrie.Brown@adfa.oz.au / 22-Feb-96