Block Ciphers (part 2)
Modern Private Key Ciphers (part 2)
FEAL
- in response to concerns about the security of DES
- and to design a cipher suitable for efficient implementation in both
software & hardware
- Japanese NTT Research Labs developed the FEAL (Fast data Encipherment
ALgorithm) in mid 1980's
A Shimizu, S Miyaguchi, "Fast Data Encipherment Algorithm FEAL", in
Advances in Cryptology - Eurocrypt'87, Lecture Notes in Computer Science, No
307, D Chaum, W Price (eds), Springer-Verlag 1988, pp 267-279
- originally specified with 4 rounds (FEAL-4)
- following cryptanalysis by other researchers was increased to 8 rounds
(FEAL-8) and now N rounds (FEAL-N), with N for highest security now 16 or 29
- also a version with a 128-bit key FEAL-NX
- a good references for FEAL-N & FEAL-NX is:
S Miyaguchi, "The FEAL Cipher Family", in Advances in Cryptology -
Crypto'90, Lecture Notes in Computer Science, No 537, A J Menezes, S A
Vanstone (eds), Springer-Verlag 1991, pp 627-638
- is one of the modern alternatives suggested for the DES, however there are
still some reservations about its security
- as with DES the design criteria are regarded as confidential by NTT and
have not been released
- FEAL consists of a key schedule and a data randomizer
- these both involve the use of functions f_(k )&
f composed of combinations of 2 S-boxes
S_(0),S_(1) that take two 8-bit inputs x,y
and create an 8-bit output
S_(d)(x,y) = ROT2((x+y+d) mod 256)
where x, y are 8-bit input values
d is 0 or 1
ROT2 is a 2-bit left rotation of an 8-bit value
- the two functions are very similar and appear as follows:
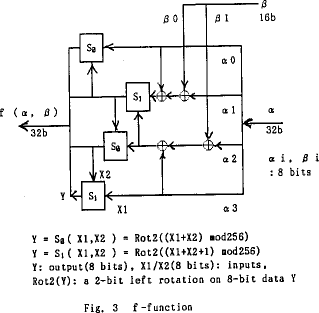
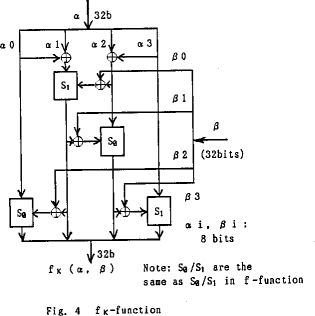
- the key schedule is constructed from f_(k )as follows:
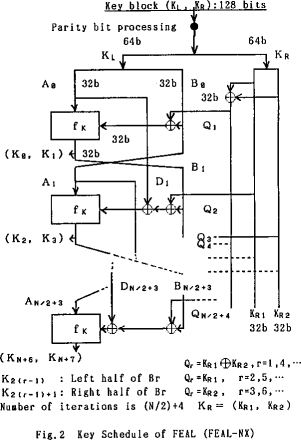
- the data randomizer is constructed from f as follows:
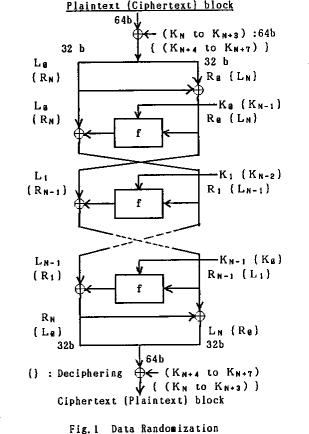
- NTT have implemented FEAL-8 in LSI hardware capable of encrypting at 96Mbps
- they have software implementations on a Intel286 running at 670 kbps
- NTT are pushing FEAL for use in a number of applications (medical,
financial, communications)
- several analyses of FEAL have been published since it was announced, these
have led to the increase in N recommended for use by FEAL (see recent Eurocrypt
& Crypto proceedings)
- FEAL has also been broken by Differential Cryptanalysis for values of
N<31, certainly for N<8 the break is fairly serious, see
E Biham, A Shamir, "Differential Cryptanalysis of FEAL and N-Hash",
in Advances in Cryptology - Eurocrypt '91, Lecture Notes in Computer Science,
vol 547, pp 1-16, D Davies (ed), Springer-Verlag, Berlin, 1991.
LOKI
- LOKI is a cipher designed at ADFA as a result of the detailed analysis of
existing block ciphers, particularly of the DES, and is the subject of Dr
Brown's PhD
L P Brown, "Analysis of the DES and the Design of the LOKI
Encryption Scheme", for Doctor of Philosophy, Department of Computer Science,
University College, University of New South Wales, Australia. Supervised by
Professor J.R. Seberry, April 1991.
- as specified originally it is known as LOKI89
- following analysis of it by ourselves and other groups, it was respecified
to improve its security as LOKI91
- the reference for the original LOKI89 is:
L P Brown, J Pieprzyk and J R Seberry, "LOKI - A Cryptographic
Primitive for Authentication and Secrecy Applications," in Advances in
Cryptology - Auscrypt '90, Lecture Notes in Computer Science, vol 453, pp
229-236, J. Seberry, J. Pieprzyk (eds), Springer-Verlag, Berlin, 1990.
L P Brown, M Kwan, J Pieprzyk, J Seberry, "Improving Resistance to
Differential Cryptanalysis and the Redesign of LOKI", Advances in Cryptology -
Asiacrypt '91, Springer-Verlag, 1992, to appear.
- several papers have been published since analysing it
- LOKI was intended to be interface compatible with the DES, so it could be
a direct replacement
- hence it uses 64-bit data and a 64-bit key (this being the minimum
resonable, and mostly compatible with DES)
- design criteria were to be published for critique
LOKI89 Design
- overall design is based on design principles developed from a detailed
analysis of the DES, including:
- permutation P and its role in growth of dependence of cipher bits on input
bits
- permutation PC2 and key rotation schedule and its role in growth of
dependence of cipher bits on key bits
- design of the LOKI S-Boxes is based on the non-linearity criteria
developed by Seberry and Pieprzyk, verified against known design criteria for
S-boxes
- aim was for structure to be as simple as possible without compromising
security
- LOKI is a Feistel class cipher, a form of Substitution-Permutation (S-P)
network (Shannon)
- key properties of such S-P networks are:
- the avalanche property
- the completeness property
- provision of these have been achieved by a two phase design
- overall structure assuming S-boxes have these properties
- S-boxes with these properties
LOKI Expansion Function E
- duplicates input + key bits to provide autoclaving
- is based on a regular selection of bits
- is designed to use 32-bit inputs for ease of software implementation
LOKI Permutation P
- sends the output bits from each S-box to the inputs of S-boxes in turn
- can be generated by a difference function on the S-box number of [+3 +2 +1
0 +3 +2 +1 0]
LOKI Key Schedule
- uses a large key rotation removing the need for PC2
- with a rotation value of 12 to match the S-box size
- with 8 rotations of each half, final key is the initial key
- 16 rounds were chosen based on Biham-Shamir results suggesting that less
would be insecure
Overall LOKI89 Structure
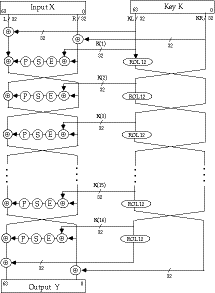
LOKI Function f
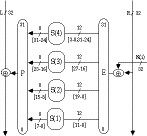
LOKI Keys
- LOKI Keys are 64-bit blocks, with no parity bits, which may be written in
hex as hhhhhhhhhhhhhhhh_(16)
- Weak, Semi-weak, and Demi-semi-weak keys are those which generate 1, 2 or
4 internal sub-keys only and which should be avoided
- for LOKI all these keys have the form:
hihihihijkjkjkjk_(16)
a total of 2^(16) out of a possible 2^(64)
LOKI S-Box Design
- a suitable family of S-boxes with avalanche and completeness properties
were required
- key principle was the concept of boolean functions with maximum
non-linearity, by Pieprzyk and Seberry
- non-linearity of a function f in the set F_(n) of all Boolean
functions of n variables, is the minimum Hamming distance between
f and the set of all linear Boolean functions L_(n) existing in F_(n)
- further they determined that exponentiation in a Galois field can be used
to form boolean functions with maximum non-linearity
LOKI89 S-Boxes
- LOKI S-boxes were chosen to have 12 inputs and 8 outputs
- to maximise growth of bit dependencies
- as largest values storable in pre-computed tables
- this is partitioned into 16 row functions with 256 columns
- each function is exponentiation in GF(2^(8) ) as follows:
Sfn_(r) = (c + r) ^(er) mod gen_(r)
- this field has 30 irreducible polynomials, and 24 exponents (of 13 inverse
pairs) which form functions of maximum non-linearity (of 112)
- a number of other exponents exist which form functions of slightly less
than maximum non-linearity, which may also be suitable for use
- exponent 31 was chosen as the smallest that gives maximum non-linearity
- 16 irreducible polynomials were chosen from the 30 available based on
tests against principles S4 to S7, the results showing little significant
variation between the alternatives.
- the resultant S-functions have non-linearities over all inputs and outputs
of between 1896 and 1936 out of a possible 1984.
- they are combined in the following structure to form the LOKI S_box:
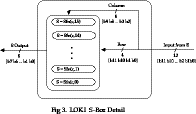
LOKI89 Cryptanalysis
- LOKI89 with up to 10 rounds can be attacked by differential cryptanalysis
using:
A.(00000510,0)->(0,00000510) always
B.(0,00000510)->(00000510,0) Pr(118/2^20)
found independently by Biham, Knudsen
- LOKI89 with up to 14 rounds can also be attacked using a 3 round
characteristic:
A.(00400000,0)->(0,00400000) always
B.(0,00400000)->(00400000,00400000) Pr(28/4096)
C.(00400000,00400000)->(00400000,0) Pr(28/4096)
found independently by Kwan, Knudsen
- LOKI89 key space is 2^60 due to the following relation:
LOKI(P, K)(+)pppppppppppppppp =
LOKI(P(+)pppppppppppppppp,K(+)mmmmmmmmnnnnnnnn)
where p=m(+)n, m,n arbitrary hex values
found independently by Biham, Knudsen, and Kwan
LOKI91 Design
- used the following additional guidelines:
- analyse key schedule to minimize generation of equivalent key, or related
(key, plaintext) pairs
- minimise probability of f(x')->0 by requiring XOR
differences giving zero output to be due to those bits permuted (by E) to more
than one S-box input
- ensure cipher has sufficient rounds so exhaustive search is the optimal
attack (ie have insufficient pairs for differential cryptanalysis)
- ensure cannot make all S-boxes give zero outputs, increasing security when
for hashing modes.
LOKI91 Specification
- the following changes were made to LOKI89
- 1
- change the key schedule so the halves were swapped after every second round
- 2
- change the key rotation schedule to alternate between ROT12 (odd rounds)
and ROT13 (even rounds)
- 3
- remove the initial and final XORs of key with plaintext and ciphertext
respectively
- 4
- alter S-box function to:
Sfn(r,c)=(c+((r*17)(+)ff_(16) )&ff_(16) )^(31
) mod gen_(r)
generator polynomials gen_(r) as in LOKI89
Overall LOKI91 Structure
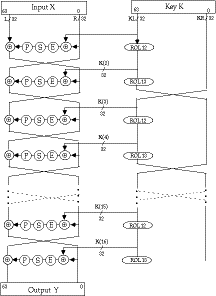
LOKI91 Cryptanalysis
- removal of initial and final XORs necessary due to other changes -
increases ciphertext dependence on key from 3 to 5 rounds, still good compared
to DES (5/7 rounds)
- key schedule changes:
- greatly reduce number of weak (*) & semi-weak keys:
Encrypt Key Decrypt key
0000000000000000 0000000000000000 *
00000000aaaaaaaa aaaaaaaa00000000
0000000055555555 5555555500000000
00000000ffffffff ffffffff00000000
aaaaaaaa00000000 00000000aaaaaaaa
aaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaa *
aaaaaaaa55555555 55555555aaaaaaaa
aaaaaaaaffffffff ffffffffaaaaaaaa
5555555500000000 0000000055555555
55555555aaaaaaaa aaaaaaaa55555555
5555555555555555 5555555555555555 *
55555555ffffffff ffffffff55555555
ffffffff00000000 00000000ffffffff
ffffffffaaaaaaaa aaaaaaaaffffffff
ffffffff55555555 55555555ffffffff
ffffffffffffffff ffffffffffffffff *
- also leave just single bit complementation property:
_________ _ _
LOKI(P,K)= LOKI(P,K)
- the S-box function redesign:
- ensures zero input gives non-zero output
- improves LOKI91 immunity to differential cryptanalysis,can be attacked in
up to
- 10 rounds using a 2 round characteristic
- f(x')->0'with Pr(122/1048576)
- 12 rounds using a 3 round characteristic
- f(x')->x'with Pr(16/4096) (twice)
- insufficient pairs to attack 16 round LOKI91
- require 2^(80 ) pairs for 3 round char
- require 2^(92 ) pairs for 2 round char
- but only have 2^(63 ) possible plaintext pairs
Latest Analysis of LOKI91
- Knudsen presented a paper at Auscrypt'92
- confirmed there are no characteristics with high enough probability to
attack LOKI91 faster than keyspace search
- showed size of image of LOKI f function is F(8,13) x
2 ^(32) significance of this is debateable
- presents chosen plaintext attack reducing exhaustive keyspace search by 4
using 2 ^(32) + 2 chosen plaintexts
- seem to confirm security of LOKI91 at present
Khufu, Khafre and Snefru
- a family of ciphers designed by Ralph Merkle from Xerox Parc labs
- some information is provided in
R C Merkle, "Fast Software Encryption Functions", in Advances in
Cryptology - Crypto'90, Lecture Notes in Computer Science, No 537, A J Menezes,
S A Vanstone (eds), Springer-Verlag 1991, pp 476-501
Khufu
- a 64-bit data and 512 bit key block cipher
- designed for bulk data encryption
- data is broken into 32-bit halves which are
- XOR'd with some key material
- go through a number of rounds of S-box lookup (lower 8 bits of Left half
to 32-bit) which is XOR'd to Right half, Left half is rotated and halves swapped
- the S-box used changes every 8 rounds
- finally halves are XOR'd with more key material
- uses the 512 bits of key to compute the S-boxes used, hence incurs a
pre-computation time on each key-change
- because it uses varying key dependent S-boxes, it is immune from
Differential Cryptanalysis
- its overall security is currently unknown
Khafre
- similar in design to Khufu
- for smaller amounts of data since no pre-computation is required
- uses fixed S-boxes and a more complex scrambling function in each round
- has been broken by Differential Cryptanalysis
Snefru
- a one-way hash function capable of reducing a message to 64, 128 or
256-bit hashes
- will consider this later
IDEA (IPES)
- developed by James Massey & Xuejia Lai at ETH originally in Zurich in
1990, then called IPES :
X Lai, J L Massey, "A Proposal for a New Block Encryption Standard"
in Advances in Cryptology - Eurocrypt '90, Lecture Notes in Computer Science,
vol 473, pp 389-404, I B Damgard (ed), Springer-Verlag, Berlin, 1991.
- was revised and published in:
X Lai, J L Massey, S Murphy, "Markov Ciphers and Differential
Cryptanalysis" in Advances in Cryptology - Eurocrypt '91, Lecture Notes in
Computer Science, vol 547, pp 17-38, D W Davies (ed), Springer-Verlag, Berlin,
1991.
- name changed to IDEA in 1992
- encrypts 64-bit blocks using a 128-bit key
- based on mixing operations from different (incompatible) algebraic groups
(XOR, Addition mod 2^(16) , Multiplication mod 2^(16) +1)
- all operations are on 16-bit sub-blocks, with no permutations used, hence
its very efficient in s/w
- IDEA is patented in Europe & US, however non-commercial use is freely
permitted
- used in the public domain PGP secure email system (with agreement from the
patent holders)
- currently no attack against IDEA is known (it appears secure against
differential cryptanalysis), and its key is too long for exhaustive search
Overview of IDEA
- IDEA encryption works as follows:
- the 64-bit data block is divided by 4 into: X_(1) , X_(2) , X_(3) , X_(4)
- in each of eight the sub-blocks are XORd, added, multiplied with one
another and with six 16-bit sub-blocks of key material, and the second and
third sub-blocks are swapped
- finally some more key material is combined with the sub-blocks
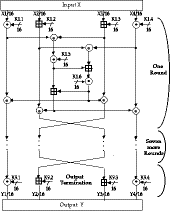
- IDEA sub-keys
- the encryption keying material is obtained by splitting the 128-bits of
key into eight 16-bit sub-keys, once these are used the key is rotated by
25-bits and broken up again etc
- the decryption keying material is a little more complex, since inverses of
the sub-blocks need to be calculated
- the keys used may be summarised as follows:
Round Encryption Keys Decryption Keys
1 K1.1 K1.2 K1.3 K1.4 K1.5 K1.6 K9.1-1 -K9.2 -K9.3 K9.4-1 K8.5
K8.6
2 K2.1 K2.2 K2.3 K2.4 K2.5 K2.6 K8.1-1 -K8.3 -K8.2 K8.4-1 K7.5
K7.6
3 K3.1 K3.2 K3.3 K3.4 K3.5 K3.6 K7.1-1 -K7.3 -K7.2 K7.4-1 K6.5
K6.6
4 K4.1 K4.2 K4.3 K4.4 K4.5 K4.6 K6.1-1 -K6.3 -K6.2 K6.4-1 K5.5
K5.6
5 K5.1 K5.2 K5.3 K5.4 K5.5 K5.6 K5.1-1 -K5.3 -K5.2 K5.4-1 K4.5
K4.6
6 K6.1 K6.2 K6.3 K6.4 K6.5 K6.6 K4.1-1 -K4.3 -K4.2 K4.4-1 K3.5
K3.6
7 K7.1 K7.2 K7.3 K7.4 K7.5 K7.6 K3.1-1 -K3.3 -K3.2 K3.4-1 K2.5
K2.6
8 K8.1 K8.2 K8.3 K8.4 K8.5 K8.6 K2.1-1 -K2.3 -K2.2 K2.4-1 K1.5
K1.6
Output K9.1 K9.2 K9.3 K9.4 K1.1-1 -K1.2 -K1.3 K1.4-1
where:
K1.1^(-1 ) is the multiplicative inverse mod 2^(16) +1
-K1.2 is the additive inverse mod 2^(16)
and the original operations are:
(+) bit-by-bit XOR
+ additional mod 2^(16) of 16-bit integers
* multiplication mod 2^(16) +1 (where 0 means 2^(16) )
IDEA Example Encryption
# Key (128-bits) Plain (64-bit) Cipher (64-bit)
7ca110454a1a6e5701a1d6d039776742 690f5b0d9a26939b 1bddb24214237ec7
idea(X=690f 5b0d 9a26 939b)
r=1, X=690f 5b0d 9a26 939b, SK=7ca1 1045 4a1a 6e57 01a1 d6d0
steps=234a 6b52 e440 840f c70a ef5d 3606 2563 0311 3917 205b e751 5245 bd18
r=2, X=205b e751 5245 bd18, SK=3977 6742 8a94 34dc ae03 43ad
steps=460a 4e93 dcd9 3995 9ad3 7706 d13d 4843 4b2d 1c6a 0d27 97f4 52f9 25ff
r=3, X=0d27 97f4 52f9 25ff, SK=a072 eece 84f9 4220 b95c 0687
steps=3320 86c2 d7f2 7410 e4d2 f2d2 57cb 4a9d 04e4 5caf 37c4 d316 da6d 28bf
r=4, X=37c4 d316 da6d 28bf, SK=5b40 e5dd 9d09 f284 4115 2869
steps=8920 b8f3 7776 69e3 fe56 d110 7266 4376 10c0 8326 99e0 67b6 3bd5 eac5
r=5, X=99e0 67b6 3bd5 eac5, SK=0eb6 81cb bb3a 13e5 0882 2a50
steps=9c69 e981 f70f 8efb 6b66 677a b63b 1db5 f5a8 abe3 69c1 02a7 4262 2518
r=6, X=69c1 02a7 4262 2518, SK=d372 b80d 9776 7427 ca11 0454
steps=d39a bab4 d9d8 75d4 0a42 cf60 ba4a 89aa d175 8bbf 02ef 08ad 310b fe6b
r=7, X=02ef 08ad 310b fe6b, SK=a1a6 e570 1a1d 6d03 4f94 2208
steps=3420 ee1d 4b28 1deb 7f08 f3f6 c124 b51a 04bd c5e1 309d 4f95 2bfc d80a
r=8, X=309d 4f95 2bfc d80a, SK=a943 4dca e034 3ada 072e ece8
steps=3df3 9d5f 0c30 0ada 31c3 9785 44a5 dc2a 7253 b6f8 4fa0 7e63 2ba7 bc22
out, X=4fa0 2ba7 7e63 bc22, SK=1152 869b 95c0 6875
= 1bdd b242 1423 7ec7
Skipjack and Clipper
- Skipjack is the cipher used in the Clipper escrowed
encryption scheme proposed by US govt
- Skipjack is a block cipher
- hardware only implementation
- 64-bit data
- 80-bit key (escrowed in 2 halves)
- 32 round
- all design details and descriptions are classified
- has been very considerable debate over its use
- attack by Matt Blaze (ATT) on the LEAF component of the Clipper protocol
for secure phone communications
Seneca
- Australia's own government use cipher is Seneca
- developed by DSTO & DSD
- a symmetric encryption algorithm "like DES"
- for govt departmental use only on sensitive but unclassified data (DES
formerly used)
- h/w only implementation at 2-20Mbps by Cima/AWA
- press release on Oct93, little other info
Other Block Ciphers
- quite a few other block ciphers have been proposed, with varying degrees
of information released on them, and with varying success against analysis
- a new (late 1993) very complete reference to many encryption algorithms
may be found in:
Bruce Schneier, "Applied Cryptography - Protocols, Algorithms and
Source Code in C", Wiley, 1994, ISBN 0-471-59756-2
- this includes source for a number of the algorithms, and a disk of source
is available in the US/Canada (but not yet elsewhere due to US export
restrictions)
- the latest information can usually be found in the proceedings of Crypto,
Eurocrypt & Asiacrypt each year, and sometimes (buried in the noise) in
sci.crypt
Differential Cryptanalysis of Block Ciphers
- Differential Cryptanalysis is a recently (in the public research
community) developed method which provides a powerful means of analysing block
ciphers
- it has been used to analyse most of the currently proposed block ciphers
with varying degrees of success
- usually have a break-even point in number of rounds of the cipher used for
which differential cryptanalysis is faster than exhaustive key-space search
- if this number is greater than that specified for the cipher, then it is
regarded as broken
- Key references are:
E Biham & A Shamir, "Differential Cryptanalysis of DES-like
Cryptosystems", Journal of Cryptology, Vol 4(1), 1991, pp3-72 Springer-Verlag.
Extended Abstract presented in Abstracts of Crypto'90
E Biham, A Shamir, "Differential Cryptanalysis of FEAL and N-Hash", in
Advances in Cryptology - Eurocrypt '91, Lecture Notes in Computer Science, vol
547, pp 1-16, D Davies (ed), Springer-Verlag, Berlin, 1991.
E Biham, A Shamir, "Differential Cryptanalysis of Snefru, Khafre, REDOC-II,
LOKI, and Lucifer", in Advances in Cryptology - Crypto '91, Lecture Notes in
Computer Science, vol 576, pp 156-171, J Feigenbaum (ed), Springer-Verlag,
Berlin, 1992.
E Biham, A Shamir, "Differential Cryptanalysis of the Full 16-round DES", in
Advances in Cryptology - Eurocrypt '92, Lecture Notes in Computer Science,
Springer-Verlag, to appear. Also as Techical Report #708, Technion - Israel
Institute of Technology, Computer Science Department, Dec 1991.
Overview of Differential Cryptanalysis
- is a statistical attack against Feistel ciphers
- uses structure in cipher not previously used
- design of S-P networks is such that the output from function f is
influenced by both input and key
R(i)=L(i-1) (+)
f(K(i)(+)R(i-1))
- hence cannot trace values back through cipher without knowing the values
of the key
- Biham & Shamir's key idea is to compare two separate encryptions
(using the same key) and look at the XOR of the S-box inputs and outputs
Ra(i)=f(K(i)(+)Ra(i-1))
Rb(i)=f(K(i)(+)Rb(i-1))
hence
Y(i)= Ra(i)(+)Rb(i)
=
f(K(i)(+)Ra(i-1)(+)K(i)(+)Rb(i-1))
= f(Ra(i-1)(+)Rb(i-1)) = f(X(i))
and this is independent of the key being used
- further various input XOR - output XOR pairs occur with different
probabilities
- hence knowing information on these pairs gives us additional information
on the cipher
XOR Profiles and Characteristics
- start by compiling a table of input vs output XOR values, an XOR
Profile for each S-box
- a particular input XOR value and output XOR value pair will occur with
some probability
- call such a specified pair, a characteristic
- can infer information about key value in one round, if find a pair
of encryptions matching a characteristic, and hence knowing input and output
XOR values
- have several variant forms of differential cryptanalysis, will discuss
just the general form used for attacking many rounds (>8) of a cipher
[4]
- can describe 1-round characteristic by:
f(x')->y', Pr(p)
(a',b')->(b',a'(+)f(b')) with prob p
i) f(0')->0', Pr(1) ie always
A.(x,0)->(0,x) always
ii) f(x')->0', Pr(p_(0) )
B.(0,x)->(x,0) with probability p_(0)
- attack multiple rounds using n-round characteristics
- n-round characteristics combine one round characteristics whose
outputs & inputs match
- probability of n-round characteristic is product of the 1-round
characteristic probabilities [5]
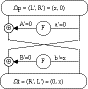2-Round Iterative Characteristic
- some common characteristic structures are:
* a 2-round characteristic:
A.(x,0)->(0,x) always
B.(0,x)->(x,0) with probability p
* a 3-round characteristic:
A.(x,0)->(0,x) always
B.(0,x)->(x,x) with probability p1
C.(x,x)->(x,0) with probability p2
- perform attack by repeatedly encrypting plaintext pairs with known input
XOR until obtain expected output XOR matching n-round characteristic being used
- if all intermediate rounds also match required XOR (which is unknown) then
have a right pair, if not then have a wrong pair, relative ratio
is S/N for attack
- assume know XOR at intermediate rounds (if right pair) then deduce keys
values for the rounds - right pairs suggest same key bits, wrong pairs give
random values
- for large numbers of rounds, probability is so low that more pairs are
required than exist with 64-bit inputs
- optimisations of this attack can be made, trading memory for search time,
and number of rounds used
- in their latest paper, Biham and Shamir show how a 13-round iterated
characteristic can be used to break the full 16-round DES
follow with Biham & Shamir TR Dec 91, Fig 1 p5, Table 2 p9
Some Sample Characteristics
DES
- the new attack on DES is based on iterating a 2 round characteristic 6.5
times with Pr(2^(-47.2) ) using:
A.(19600000,0)->(0,19600000) always
B.(0,19600000)->(19600000,0) Pr(1/234)
LOKI89
- LOKI89 with up to 10 rounds can be attacked by differential cryptanalysis
using:
A.(00000510,0)->(0,00000510) always
B.(0,00000510)->(00000510,0) Pr(118/2^20)
LOKI91
- LOKI91 with up to 10 rounds can be attacked by differential cryptanalysis
using 2 round characteristic:
A.(x,0)->(0,x) always
B.(0,x)->(x,0) Pr(122/2^20)
- LOKI91 with up to 12 rounds can be attacked by differential cryptanalysis
using 3 round characteristic:
A.(x,0)->(0,x) always
B.(0,x)->(x,x) Pr(16/4096)
C.(x,x)->(x,0) Pr(16/4096)
- Knudsen has proved that no 13 round characteristic exist for LOKI91
Why Flat XOR Profiles Dont Work
- one suggested criteria to improve immunity to differential cryptanalysis
was to use a flat XOR profile (Dawson & Tavares)
- designed with constant probabilities
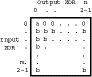Flat XOR Profile
- usually results in a weaker cipher
- can build a 2 round iterative characteristic, changing bits to one S-box
only
- know this will occur with Pr (^(1) /_(2) n)
- then iterate over 2k rounds with Pr (^(1) /_(2) kn)
- eg for DES like scheme: m=6, n=4, k=8,
- hence break with Pr (^(1) /_(2) 28)
- consequently need to use additional design criteria such as those
specified in design of LOKI91
Linear Cryptanalysis of Block Ciphers
- Linear Cryptanalysis is another recently developed method for analysing
block ciphers
- like differential cryptanalysis it is a statistical method
- again have a break-even point in number of rounds of the cipher used for
which linear cryptanalysis is faster than exhaustive key-space search
- if this number is greater than that specified for the cipher, then it is
regarded as broken
- Key references are:
Matsui M, "Linear Cryptanalysis Method for DES Cipher", in Advances
in Cryptology - Eurocrypt '93, Lecture Notes in Computer Science, vol 765, pp
386-397, T Helleseth (ed), Springer-Verlag, Berlin, 1994.
Tokita T, Sorimachi T, Matsui M "Linear Cryptanalysis of LOKI and s^(2)
DES", in Advances in Cryptology - Asiacrypt '94, Lecture Notes in Computer
Science, vol 917, pp 293-303, J Pieprzyk, R Safavi-Naini (eds),
Springer-Verlag, Berlin, 1995.
Ohta K, Moriai S, Aoki K, "Improving the Search Algorithm for the Best
Linear Expression", in Advances in Cryptology - Crypto '95, Lecture Notes in
Computer Science, vol 963, pp 157-170, D Coppersmith (ed), Springer-Verlag,
Berlin, 1995.
- in Linear Cryptanalysis want to find a linear approximation which holds
with Prob p!=^(1) /_(2)
P[i1,i2,...,ia](+)C[j1,j2,...,jb]=K[k1,k2,...,kc]
where ia,jb,kc are bit locations in P,C,K
- can determine one bit of key using maximum likelihood algorithm, using a
large number of trial encryptions
- effectiveness of linear cryptanalysis is given by
|p - 1/2|
- DES can be broken by encrypting 2^(47) known plaintexts
PL[7,18,24](+) PR[12,16](+) CL[15](+) CR[7,18,24,29](+) F16(CR,K16)[15] = K1[19,23](+)K3[22](+) K4[44](+) K5[22](+)K7[22](+) K8[44](+) K9[22](+) K11[22](+) K12[44](+) K13[22](+) K15[22]
- this will recover some of the key bits, the rest must be searched for
exhaustively
- LOKI with 12 or more rounds cannot be broken using linear cryptanalysis
Stream Ciphers and the Vernam cipher
- process the message bit by bit (as a stream)
- the most famous of these is the Vernam cipher
- (also known as the one-time pad)
- invented by Vernam, working for AT&T, in 1917
- simply add bits of message to random key bits
- need as many key bits as message, difficult in practise
- (ie distribute on a mag-tape or CDROM)
- is unconditionally secure provided key is truly random
- suggest generating keystream from a smaller (base) key
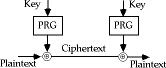
- use some pseudo-random function to do this
Stream Ciphers and Pseudo-Random Generators
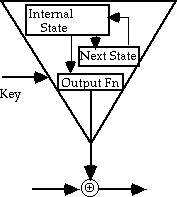
- although this looks very attractive, it proves to be very very difficult
in practise to find a good pseudo-random function that is cryptographically
strong
- generated stream must be
- statistically random (like result of coin tossing)
- (know part of seq not enough)
- PRG may be controlled just by key influencing:
- next-state function (output feedback mode)
- output function (counter mode)
- PRG may be controlled both by data and key:
- output function (cipher feedback mode)
- can use a block cipher as a PRG (cf CFB, OFB modes)
- believe can construct much more efficient PRGs though
Linear Feedback Shift Registers
- linear feedback shift registers (LFSRs) are often proposed for use as a
PRG in stream ciphers
- uses a shift register (of binary bits) of some length
- each time a bit is needed, all bits are shifted one place
- the bit bumped out is the bit used
- a new bit is formed from a linear function of other bits
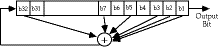
- key is the initial state (value) in the shift register and the feedback
function used
- with the correct function, an n-bit shift register can generate a sequence
of 2^(32 ) -1 bits
- need to use a primitive polynomial linear function
- this is easy to code, very fast to run in h/w and s/w
- BUT is insecure - statistically random but predictable
- just 2n bits is enough to completely predict sequence
- LFSRs do form the basis though of most stream ciphers, which attempt to
hide the underlying LFSR structure
Stream Ciphers Based on LFSRs
- Rueppel has codified stream ciphers design criteria:
- long period with no repetitions
- large linear complexity (based on size of equiv LFSR)
- statistically random
- confusion (output bits depend on all key bits)
- diffusion
- use of highly non-linear boolean functions
- a number of proposals exist
- combine outputs of several LFSRs in a multiplexor
- control the clocking of some LFSRs by another
- only select some of the output bits (many clocks each)
- virtually all of these proposals have identified flaws
- ANY stream generator can be modelled by an LFSR of some size using the
Berlecamp-Massey algorithm
- practically today, if LFSRs are used, they are re-keyed extremely often
(fast enough so attacks will yeild little info, slow enough for a block cipher
to be used to create keying information)
Other Stream Ciphers
RC4
- a cipher created by RSA Data Security Inc
- commercial cipher, but details have leaked
- basically it:
- turns the key into a random permutation
- uses that permutation to scamble input info
- see
ftp:///ftp.dsi.unimi.it/pub/security/crypt/code/
rc4.revealed.gz
ftp:///ftp.dsi.unimi.it/pub/security/crypt/code/
rc4.schneier.test.gz
Public Key Based Schemes
- have several schemes based on public key algorithms, eg RSA
- simplest, best, known and most efficient is the "Blum, Blum and Shub"
(BBS) generator
x_(i+1) = x_(i) ^(2 ) mod n and use b_(i) the LSB of x_(i)
where n=p.q, primes p,q=3 mod 4
- security rests on difficulty of factoring N
- is unpredictable given any run of bits
- is slow (since very large numbers must be used for security), too slow for
cipher use, good for key gen
[4] Biham & Shamir JC 4(1) 91 Table 2 p12, Table 3 p13
[5] Biham & Shamir JC 4(1) 91 DES characterisitcs p18;
Table 11 p37, Table 12 p41
[CSC Info]
Lawrie.Brown@adfa.oz.au / 15-Apr-96