Block Ciphers (part 1)
Modern Private Key Ciphers (part 1)
- now want to concentrate on modern encryption systems
- these usually consider the message as a sequence of bits
- (eg as a series of ASCII characters concatenated)
- have two broad families of methods
- stream ciphers and block ciphers
Stream Ciphers and the Vernam cipher
- process the message bit by bit (as a stream)
- the most famous of these is the Vernam cipher
- (also known as the one-time pad)
- invented by Vernam, working for AT&T, in 1917
- simply add bits of message to random key bits
- need as many key bits as message, difficult in practise
- (ie distribute on a mag-tape or CDROM)
- is unconditionally secure provided key is truly random

- since difficult to distribute so much key, why not generate keystream from
a smaller (base) key
- use some pseudo-random function to do this
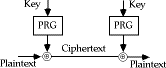
- although this looks very attractive, it proves to be very very difficult
in practise to find a good pseudo-random function that is cryptographically
strong
- this is still an area of much research
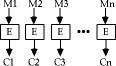
Block Ciphers
- in a block cipher the message is broken into blocks, each of which is then
encrypted (ie like a substitution on very big characters - 64-bits or more)
- most modern ciphers we will study are of this form
Shannons Theory of Secrecy Systems
- Claude Shannon wrote some of the pivotal papers on modern cryptology
theory in 1949:
- C E Shannon, "Communication Theory of Secrecy Systems", Bell System
Technical Journal, Vol 28, Oct 1949, pp 656-715
- C E Shannon, "Prediction and Entropy of printed English", Bell System
Technical Journal, Vol 30, Jan 1951, pp 50-64
- in these he developed the concepts of:
- entropy of a message,
- redundancy in a language,
- theories about how much information is needed to break a cipher
- defined the concepts of computationally secure vs unconditionally secure
ciphers
- he showed that the Vernam cipher is the only currently known
unconditionally secure cipher, provided the key is truly random
- also showed that if try to encrypt English text by adding to other English
text (ie a Bookcipher), this is not secure since English is 80%
redundant, giving ciphertext with 60% redundancy, enough to break
- a similar technique can also be used if the same random key stream is used
twice on different messages, the redundancy in the messages is sufficient to
break this
- as discussed earlier, exhaustive key search is the most fundamental
attack, and is directly proportional to the size of the key
- can tabulate these for reasonable assumptions about the number of
operations possible (& parallel tests):
Key Size (bits) Time (1us/test) Time (1us/106test)
24 8.4 sec 8.4 usec
32 35.8 mins 2.15 msec
40 6.4 days 550 msec
48 4.46 yrs 2.35 mins
56 ~2000 yrs 10.0 hrs
64 ~500000 yrs 107 days
- as the ultimate limit, it can be shown from energy consumption
considerations that the maximum number of possible elementary operations in
1000 years is about: 3 x 10 ^(48)
- similarly can show that if need say 10 atoms to store a bit of
information, then the greatest possible number of bits storable in a volume of
say the moon is: 10 ^(45)
- if a cipher requires more operations, or needs more storage than
this, it is pretty reasonable to say it is computationally secure
- eg to test all possible 128-bit keys in Lucifer takes about 3
x 10 ^(48) encryptions, needing 10 ^(19)
years
Substitution-Permutation Ciphers
- in his 1949 paper Shannon also introduced the idea of
substitution-permutation (S-P) networks, which now form the basis of modern
block ciphers
- an S-P network is the modern form of a substitution-transposition product
cipher
- S-P networks are based on the two primitive cryptographic operations we
have seen before
Substitution Operation
- a binary word is replaced by some other binary word
- the whole substitution function forms the key
- if use n bit words, the key is 2^(n)!bits,
grows rapidly
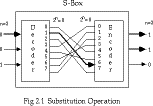
- can also think of this as a large lookup table, with n address lines
(hence 2^(n) addresses), each n bits wide being the
output value
- will call them S-boxes
Permutation Operation
- a binary word has its bits reordered (permuted)
- the re-ordering forms the key
- if use n bit words, the key is n!bits, which grows more
slowly, and hence is less secure than substitution
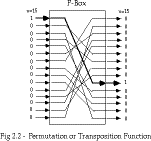
- this is equivalent to a wire-crossing in practise (though is much harder
to do in software)
- will call these P-boxes
Substitution-Permutation Network
- Shannon combined these two primitives
- he called these mixing transformations
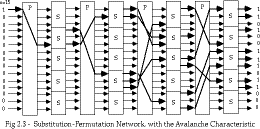
- Shannons mixing transformations are a special form of product ciphers where
- S-Boxes
- provide confusion of input bits
- P-Boxes
- provide diffusion across S-box inputs
- in general these provide the following results, as described in:
A F Webster & S E Tavares "On the Design of S-boxes", in
Advances in Cryptology - Crypto 85, Lecture Notes in Computer Science, No 218,
Springer-Verlag, 1985, pp 523-534
Avalanche effect
- where changing one input bit results in changes of approx
half the output bits
More formally, a function f has a good avalanche effect if
for each bit i,0<=i<m, if the 2^(m)
plaintext vectors are divided into 2^(m-1) pairs X
and X_(i) with each pair differing only in bit
i; and if the 2^(m-1) exclusive-or sums, termed
avalanche vectors
V_(i) = f(X) (+)
f(X_(i))
are compared, then about half of these sums should be found to be 1.
Completeness effect
- where each output bit is a complex function of all the input bits
More formally, a function f has a good completeness
effect if for each bit j,0<=j<m, in the ciphertext
output vector, there is at least one pair of plaintext vectors X and
X_(i) which differ only in bit i, and for which
f(X) and f(X_(i)) differ in bit j
Practical Substitution-Permutation Networks
- in practise we need to be able to decrypt messages, as well as to encrypt
them, hence either:
- have to define inverses for each of our S & P-boxes, but this doubles
the code/hardware needed, or
- define a structure that is easy to reverse, so can use basically the same
code or hardware for both encryption and decryption
- Horst Feistel, working at IBM Thomas J Watson Research Labs devised just
such a structure in early 70's, which we now call a feistel cipher
- the idea is to partition the input block into two halves,
L(i-1)and R(i-1), and use only R(i-1)in each round
i (part) of the cipher
- the function g incorporates one stage of the S-P network,
controlled by part of the key K(i)known as the ith
subkey
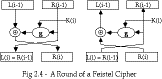
- this can be described functionally as:
L(i) = R(i-1)
R(i) = L(i-1) (+) g(K(i), R(i-1))
- this can easily be reversed as seen in the above diagram, working
backwards through the rounds
- in practise link a number of these stages together (typically 16 rounds)
to form the full cipher
Lucifer
- Lucifer is the first publically known example of a practical
substitution-permutation cipher
- it was developed by Horst Feistel at IBM labs
- the best known public reference is his paper:
- Horst Feistel, "Cryptography and Computer Privacy", Scientific American,
Vol 228(5), May 1973, pp 15-23.
- it provides an overview of his work, but actual details of Lucifer are
very sketchy, the best detailed reference:
- Arthur Sorkin, "Lucifer, A Cryptographic Algorithm", Cryptologia, Vol
8(1), Jan 1984, pp 22-41, with addenda in Vol 8(3) pp260-261
- this contains a detailed description of the algorithm, plus a Fortran
implementation
- the original descriptions are not the clearest
Sorkin Fig 1 p24
- redrawn in modern form, Lucifer has the following form:
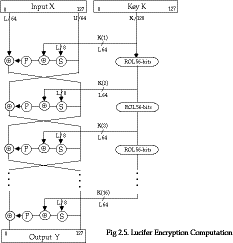
- Lucifer uses 128-bit data blocks and 128-bit keys, and uses a Feistel
structure
- the subkeys used in each round are taken from the left part of the key,
which is then rotated left 56-bits, so all key bits are used
- the S-P function for Lucifer has the following structure:
- the substitution consists of 8 identical pairs of 4-bit S-boxes (S0 &
S1) used in alternate order (S0|S1) or (S1|S0) depending on the key
- then the subkey is added modulo 2
- and the result is permuted through a combination of small 8-bit
permutations and a large 128-bit simple permutation (convolution)
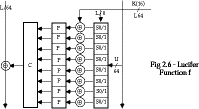
- for details see Sorkin
- from the little known discussion, Lucifer appears to be a fairly well
constructed cipher, although recently it has been theorectically broken by
differential cryptanalysis
- its main claim is that it is the predecessor the DES, developed by IBM in
the mid 70's and submitted to the NBS (& NSA) to become the standard
encryption algorithm for commercial use at the time
DES
- in May 1973, and again in Aug 1974 the NBS (now NIST) called for possible
encryption algorithms for use in unclassified government applications
- response was mostly disappointing, however IBM submitted their Lucifer
design
- following a period of redesign and comment it became the Data Encryption
Standard (DES)
- it was adopted as a (US) federal standard in Nov 76, published by NBS as a
hardware only scheme in Jan 77 and by ANSI for both hardware and software
standards in ANSI X3.92-1981 (also X3.106-1983 modes of use)
- subsequently it has been widely adopted and is now published in many
standards around the world
- cf Australian Standard AS2805.5-1985
- one of the largest users of the DES is the banking industry, particularly
with EFT, and EFTPOS
- it is for this use that the DES has primarily been standardised, with ANSI
having twice reconfirmed its recommended use for 5 year periods - a further
extension is not expected however
- although the standard is public, the design criteria used are classified
and have yet to be released
- there has been considerable controversy over the design, particularly in
the choice of a 56-bit key
- W Diffie, M Hellman "Exhaustive Cryptanalysis of the NBS Data Encryption
Standard" IEEE Computer 10(6), June 1977, pp74-84
- M Hellman "DES will be totally insecure within ten years" IEEE Spectrum
16(7), Jul 1979, pp 31-41
- recent analysis has shown despite this that the choice was appropriate,
and that DES is well designed
- rapid advances in computing speed though have rendered the 56 bit key
susceptible to exhaustive key search, as predicted by Diffie & Hellman
- the DES has also been theorectically broken using a method called
Differential Cryptanalysis, however in practise this is unlikely to be a
problem (yet)
Overview of the DES Encryption Algorithm
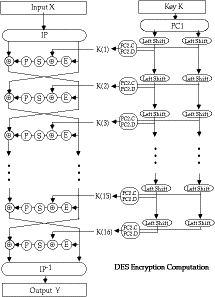
- the basic process in enciphering a 64-bit data block using the DES
consists of:
- an initial permutation (IP)
- 16 rounds of a complex key dependent calculation f
- a final permutation, being the inverse of IP
- in more detail the 16 rounds of f consist of:
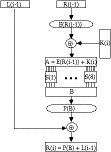
- this can be described functionally as
L(i) = R(i-1)
R(i) = L(i-1) (+) P(S( E(R(i-1))(+)
K(i) ))
and forms one round in an S-P network
- the subkeys used by the 16 rounds are formed by the key schedule
which consists of:
- an initial permutation of the key (PC1) which selects 56-bits in two
28-bit halves
- 16 stages consisting of
- selecting 24-bits from each half and permuting them by PC2 for use in
function f,
- rotating each half either 1 or 2 places depending on the key rotation
schedule KS
- this can be described functionally as:
K(i) = PC2(KS(PC1(K),i))
- the key rotation schedule KS is specified as:
Round 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
KS 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
Total Rot 1 2 4 6 8 10 12 14 15 17 19 21 23 25 27 28
- more details on the various DES functions can be found in your textbooks
- following is a walk-through of a DES encryption calculation taken from:
H Katzan, "The Standard Data Encryption Algorithm", Petrocelli
Books, New York, 1977
DES Modes of Use
- DES encrypts 64-bit blocks of data, using a 56-bit key
- we need some way of specifying how to use it in practise, given that we
usually have an arbitrary amount of information to encrypt
- the way we use a block cipher is called its Mode of Use and four
have been defined for the DES by ANSI in the standard: ANSI X3.106-1983 Modes
of Use)
- modes are either:
- Block Modes
- splits messages in blocks (ECB, CBC)
- Stream Modes
- on bit stream messages (CFB, OFB)
Block Modes
- Electronic Codebook Book (ECB)
- - where the message is broken into independent 64-bit blocks which are
encrypted
C_(i) = DES_(K1) (P_(i))
- Cipher Block Chaining (CBC)
- - again the message is broken into 64-bit blocks, but they are linked
together in the encryption operation with an IV
C_(i) = DES_(K1)
(P_(i)(+)C_(i-1))
C_(-1)=IV
Stream Modes
- Cipher FeedBack (CFB)
- - where the message is treated as a stream of bits, added to the output of
the DES, with the result being feed back for the next stage
C_(i) = P_(i)(+)
DES_(K1) (C_(i-1)) C_(-1)=IV
- Output FeedBack (OFB)
- - where the message is treated as a stream of bits, added to the message,
but with the feedback being independent of the message
C_(i) = P_(i)(+)
O_(i) O_(i) = DES_(K1)(O_(i-1))
O_(-1)=IV
- each mode has its advantages and disadvantages
- []
Limitiations of Various Modes
ECB
- repetitions in message can be reflected in ciphertext
- if aligned with message block
- particularly with data such graphics
- or with messages that change very little, which become a code-book
analysis problem
- weakness is because enciphered message blocks are independent of each other
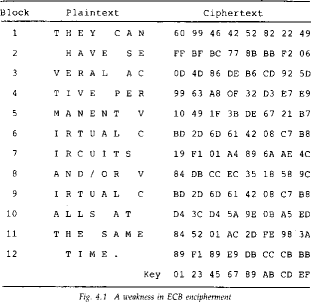 Davies Fig 4.1 p81
Davies Fig 4.1 p81
CBC
- use result of one encryption to modify input of next
- hence each ciphertext block is dependent on all message blocks
before it
- thus a change in the message affects the ciphertext block after the change
as well as the original block
Davies Fig 4.5 p85
- to start need an Initial Value (IV) which must be known by both
sender and receiver
- however if IV is sent in the clear, an attacker can change bits of the
first block, and change IV to compensate
- hence either IV must be a fixed value (as in EFTPOS) or it must be sent
encrypted in ECB mode before rest of message
- also at the end of the message, have to handle a possible last short block
- either pad last block (possible with count of pad size), or use some
fiddling to double up last two blocks
- see Davies for examples
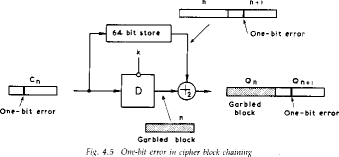
CFB
- when data is bit or byte oriented, want to operate on it at that level, so
use a stream mode
- the block cipher is use in encryption mode at both ends,
with input being a feed-back copy of the ciphertext
- can vary the number of bits feed back, trading off efficiency for ease of
use
- again errors propogate for several blocks after the error
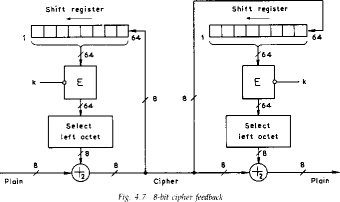
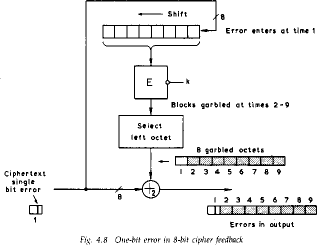 Davies Fig 4.7 p88 & Fig 4.8 p89
Davies Fig 4.7 p88 & Fig 4.8 p89
OFB
- also a stream mode, but intended for use where the error feedback is a
problem, or where the encryptions want to be done before the message is
available
- is superficially similar to CFB, but the feedback is from the output of
the block cipher and is independent of the message, a variation of a Vernam
cipher
- again an IV is needed
- sender and receiver must remain in sync, and some recovery method is
needed to ensure this occurs
- although originally specified with varying m-bit feedback in the
standards, subsequent research has shown that only 64-bit OFB should
ever be used (and this is the most efficient use anyway), see
D Davies, G Parkin, "The Average Cycle Size of the Key Stream in
Output Feedback Encipherment" in Advances in Cryptology - Crypto 82, Plenum
Press, 1982, pp97-98
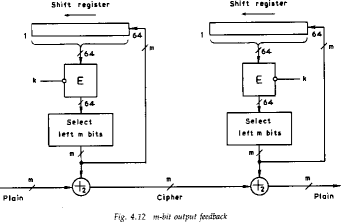 Davies Fig 4.12 p94
Davies Fig 4.12 p94
DES Weak Keys
- with many block ciphers there are some keys that should be avoided,
because of reduced cipher complexity
- these keys are such that the same sub-key is generated in more than one
round, and they include:
Weak Keys
- he same sub-key is generated for every round
- DES has 4 weak keys
Semi-Weak Keys
- only two sub-keys are generated on alternate rounds
- DES has 12 of these (in 6 pairs)
Demi-Semi Weak Keys
- have four sub-keys generated
- none of these cause a problem since they are a tiny fraction of all
available keys
- however they MUST be avoided by any key generation program [2]
DES Design Principles
- although the standard for DES is public, the design criteria used are
classified and have yet to be released
- some information is known, and more has been deduced
L P Brown, "A Proposed Design for an Extended DES", in Computer
Security in the Age of Information, W. J. Caelli (ed), North-Holland, pp 9-22,
1989
L P Brown, J R Seberry, "On the Design of Permutation Boxes in DES Type
Cryptosystems", in Advances in Cryptology - Eurocrypt '89, Lecture Notes in
Computer Science, vol 434, pp 696-705, J.J. Quisquater, J. Vanderwalle (eds),
Springer-Verlag, Berlin, 1990.
L P Brown and J R Seberry, "Key Scheduling in DES Type Cryptosystems," in
Advances in Cryptology - Auscrypt '90, Lecture Notes in Computer Science, vol
453, pp 221-228, J. Seberry, J. Pieprzyk (eds), Springer-Verlag, Berlin, 1990.
- will briefly overview the basic results, for more detailed analyses see
the above papers
DES S-Box Design Criteria
- each S-box may be considered as four substitution functions
- these 1-1 functions map inputs 2,3,4,5 onto output bits
- a particular function is selected by bits 1,6
- this provides an autoclave feature
DES Design Criteria
- there were 12 criterion used, resulting in about 1000
- possible S-Boxes, of which the implementers chose 8
- these criteria are CLASSIFIED SECRET
- however, some of them have become known
- The following are design criterion:
R1: Each row of an S-box is a permutation of 0 to 15
R2: No S-Box is a linear of affine function of the input
R3: Changing one input bit to an S-box results in changing at least two
output bits
R4: S(x) and S(x+001100) must differ in at least 2 bits
- The following are said to be caused by design criteria
R5: S(x) [[pi]] S(x+11ef 00) for any choice of e and
f
R6: The S-boxes were chosen to minimize the difference between the
number of 1's and 0's in any S-box output when any single input is held constant
R7: The S-boxes chosen require significantly more minterms than a random
choice would require
Meyer Tables 3-17, 3-18
DES Permutation Tables
- there are 5 Permutations used in DES:
- IP and IP^(-1) , P, E, PC1, PC2
- their design criteria are CLASSIFIED SECRET
- it has been noted that IP and IP^(-1) and PC1 serve
no cryptological function when DES is used in ECB or CBC modes, since searches
may be done in the space generated after they have been applied
- E, P, and PC2 combined with the S-Boxes must supply the
required dependence of the output bits on the input bits and key bits
(avalanche and completeness effects)
Ciphertext Dependence on Input and Key
- the role of P, E, and PC2 is distribute the outputs of the
S-boxes so that each output bit becomes a function of all the input bits in as
few rounds as possible
- Carl Meyer (in Meyer 1978, or Meyer & Matyas 1982) performed this
analysis on the current DES design
Ciphertext dependence on Plaintext
- define G_(i,j) a 64*64 array which shows the dependence of output
bits X(j) on input bits X(i)
- examine G_(0,j) to determine how fast complete dependence is
achieved
- to build G_(0,1) use the following
L(i) = R(i-1)
R(i) = L(i-1) (+) f( K(i), R(i-1))
- DES P reaches complete dependence after 5 rounds
- []
Ciphertext dependence on Key
- Carl Meyer also performed this analysis
- define F_(i,j) a 64*56 array which shows the dependence of output
bits X(j) on key bits U(i) (after PC1 is used)
- examine F_(0,j) to determine how fast complete dependence is
achieved
- DES PC2 reaches complete dependence after 5 rounds
Key Scheduling and PC2
- Key Schedule
- is a critical component in the design
- must provide different keys for each round otherwise security may be
compromized (see Grossman & Tuckerman 1978)
- current scheme can result in weak keys which give the same, 2 or 4 keys
over the 16 rounds
- Key Schedule and PC-2 Design
- is performed in two 28-bit independent halves
- C-side provides keys to S-boxes 1 to 4
- D-side provides keys to S-boxes 5 to 8
- the rotations are used to present different bits of the key for selection
on successive rounds
- PC-2 selects key-bits and distributes them over the S-box inputs
Possible Techniques for Improving DES
- multiple enciphering with DES
- extending DES to 128-bit data paths and 112-bit keys
- extending the Key Expansion calculation
Triple DES
- DES variant
- standardised in ANSI X9.17 & ISO 8732 and in PEM for key management
- proposed for general EFT standard by ANSI X9
- backwards compatible with many DES schemes
- uses 2 or 3 keys
C = DES_(K1) Bbc{(DES^(-1)_(K2)Bbc{(DES_(K1)(P)))
- no known practical attacks
- brute force search impossible
- meet-in-the-middle attacks need 2^(56) PC pairs per key
- popular current alternative
[1] follow with Modes of Use illustrations
[2] follow with Appendix A from AS2805.5 (also found in
Seberry Appendix B2)
[3] follow with Meyer - Fig 3-17; Fig 3-15, 3-16, 3-19; Fig
3-18, 3-21.
[CSC Info]
Lawrie.Brown@adfa.oz.au / 15-Apr-96
 Davies Fig 4.1 p81
Davies Fig 4.1 p81











 Davies Fig 4.1 p81
Davies Fig 4.1 p81


 Davies Fig 4.7 p88 & Fig 4.8 p89
Davies Fig 4.7 p88 & Fig 4.8 p89
 Davies Fig 4.12 p94
Davies Fig 4.12 p94