Authentication, Hash Functions, Digital
Signatures
Message Authentication
- message authentication is concerned with:
- protecting the integrity of a message
- validating identity of originator
- non-repudiation of origin (dispute resolution)
- electronic equivalent of a signature on a message
- an authenticator, signature, or message authentication
code (MAC) is sent along with the message
- the MAC is generated via some algorithm which depends on both the message
and some (public or private) key known only to the sender and receiver
- the message may be of any length
- the MAC may be of any length, but more often is some fixed size, requiring
the use of some hash function to condense the message to the required
size if this is not acheived by the authentication scheme
- need to consider replay problems with message and MAC
- require a message sequence number, timestamp or negotiated random values

Authentication using Private-key Ciphers
- if a message is being encrypted using a session key known only to the
sender and receiver, then the message may also be authenticated
- since only sender or receiver could have created it
- any interference will corrupt the message (provided it includes sufficient
redundancy to detect change)
- but this does not provide non-repudiation since it is impossible to prove
who created the message
- message authentication may also be done using the standard modes of use of
a block cipher
- sometimes do not want to send encrypted messages
- can use either CBC or CFB modes and send final block, since this will
depend on all previous bits of the message
- no hash function is required, since this method accepts arbitrary length
input and produces a fixed output
- usually use a fixed known IV
- this is the approached used in Australian EFT standards AS8205
- major disadvantage is small size of resulting MAC since 64-bits is
probably too small
Hashing Functions
- hashing functions are used to condense an arbitrary length message to a
fixed size, usually for subsequent signature by a digital signature algorithm
- good cryptographic hash function h should have the following properties:
- h should destroy all homomorphic structures in the underlying public key
cryptosystem (be unable to compute hash value of 2 messages combined given
their individual hash values)
- h should be computed on the entire message
- h should be a one-way function so that messages are not disclosed by their
signatures
- it should be computationally infeasible given a message and its hash value
to compute another message with the same hash value
- should resist birthday attacks (finding any 2 messages with the
same hash value, perhaps by iterating through minor permutations of 2 messages
[1])
- it is usually assumed that the hash function is public and not keyed
- traditional CRCs do not satisfy the above requirements
- length should be large enough to resist birthday attacks (64-bits is now
regarded as too small, 128-512 proposed)
Snefru
- a one-way hash function designed by Ralph Merkle
- creates 128 or 256 bit long hash values (let m be length)
- uses an algorithm H which hashes 512-bits to m-bits, taking the first m
output bits of H as the hash value
- H is based on a reversible block cipher E operating on 512-bit blocks
- H is the last m-bits of the output of E XOR'd with the first m-bits of the
input of E
- E is composed of several passes, each pass has 64 rounds of an S-box
lookup and XOR
- E can use 2 to 8 passes
- overview of algorithm
- break message into 512-m bit chunks
- each chunk has the previous hash value appended (assuming an IV of 0)
- H is computed on this value, giving a new hash value
- after the last block (0 padded to size as needed) the hash value is
appended to a message length value and H computed on this, the resulting value
being the MAC
- Snefru has been broken by a birthday attack by Biham and Shamir for
128-bit hashes, and possibly for 256-bit when 2 to 4 passes are used in E
- Merkle recommends 8 passes, but this is slow
MD2, MD4 and MD5
- family of one-way hash functions by Ronald Rivest
- MD2 is the oldest, produces a 128-bit hash value, and is regarded as
slower and less secure than MD4 and MD5
- MD4 produces a 128-bit hash of the message, using bit operations on 32-bit
operands for fast implementation
R L Rivest, "The MD4 Message Digest Algorithm", Advances in Cryptology -
Crypto'90, Lecture Notes in Computer Science No 537, Springer-Verlag 1991,
pp303-311
- MD4 overview
- pad message so its length is 448 mod 512
- append a 64-bit message length value to message
- initialise the 4-word (128-bit) buffer (A,B,C,D)
- process the message in 16-word (512-bit) chunks, using 3 rounds of 16 bit
operations each on the chunk & buffer
- output hash value is the final buffer value
- some progress at cryptanalysing MD4 has been made, with a small number of
collisions having been found
- MD5 was designed as a strengthened version, using four rounds, a little
more complex than in MD4 [2]
- a little progress at cryptanalysing MD5 has been made with a small number
of collisions having been found
- both MD4 and MD5 are still in use and considered secure in most practical
applications
- both are specified as Internet standards (MD4 in RFC1320, MD5 in RFC1321)
SHA (Secure Hash Algorithm)
- SHA was designed by NIST & NSA and is the US federal standard for use
with the DSA signature scheme (nb the algorithm is SHA, the standard is SHS)
- it produces 160-bit hash values
- SHA overview[3]
- pad message so its length is a multiple of 512 bits
- initialise the 5-word (160-bit) buffer (A,B,C,D,E) to
- (67452301,efcdab89,98badcfe,10325476,c3d2e1f0)
- process the message in 16-word (512-bit) chunks, using 4 rounds
of 20 bit operations each on the chunk & buffer
- output hash value is the final buffer value
- SHA is a close relative of MD5, sharing much common design, but each
having differences
- SHA has very recently been subject to modification following NIST
identification of some concerns, the exact nature of which is not public
- current version is regarded as secure
Other Hash Functions
HAVAL
- a variable length one-way hash function designed by Uni of Wollongong and
recently published at Auscrypt'92
- it processes messages in 1024-bit blocks, using an 8-word buffer and 3 to
5 rounds of 16 steps each, creating hash values of 128, 160, 192, 224, or 256
bits in length
- uses highly non-linear 7-variable functions in each step
- is faster than MD5
- it not subject to MD5 type analysis, no attack is known
Using Private Key Ciphers
- a large number of "Modes of Use" have been proposed which use a block
cipher to create a hash value
- original proposal was by Davies and Meyer
- many other proposals
- most have been broken using a birthday attack
- the design of fast, secure hash functions of this form is still being
studied, with many questions unresolved
Digital Signature Schemes
- public key signature schemes
- the private-key signs (creates) signatures, and the public-key verifies
signatures
- only the owner (of the private-key) can create the digital signature,
hence it can be used to verify who created a message
- anyone knowing the public key can verify the signature (provided they are
confident of the identity of the owner of the public key - the key distribution
problem)
- usually don't sign the whole message (doubling the size of information
exchanged), but just a hash of the message
- digital signatures can provide non-repudiation of message origin, since an
asymmetric algorithm is used in their creation, provided suitable timestamps
and redundancies are incorporated in the signature
RSA
- RSA encryption and decryption are commutative, hence it may be used
directly as a digital signature scheme
- given an RSA scheme {(e,R), (d,p,q)}
- to sign a message, compute:
- to verify a signature, compute:
- M = Se(mod R) = Me.d(mod R) = M(mod R)
- thus know the message was signed by the owner of the public-key
- would seem obvious that a message may be encrypted, then signed using RSA
without increasing it size
- but have blocking problem, since it is encrypted using the receivers
modulus, but signed using the senders modulus (which may be smaller)
- several approaches possible to overcome this
- more commonly use a hash function to create a separate MDC which is then
signed
El Gamal Signature Scheme
- whilst the ElGamal encryption algorithm is not commutative, a closely
related signature scheme exists
- El Gamal Signature scheme
- given prime p, public random number g, private (key) random number x,
compute
- public key is (y,g,p)
- nb (g,p) may be shared by many users
- p must be large enough so discrete log is hard
- private key is (x)
- to sign a message M
- choose a random number k, GCD(k,p-1)=1
- compute
- a = gk(mod p)
- use extended Euclidean (inverse) algorithm to solve
- M = x.a + k.b (mod p-1)
- the signature is (a,b), k must be kept secret
- (like ElGamal encryption is double the message size)
- to verify a signature (a,b) confirm:
Example of ElGamal Signature Scheme
- given p=11, g=2
- choose private key x=8
- compute
- y = gx(mod p) = 28(mod 11) = 3
- public key is y=3,g=2,p=11)
- to sign a message M=5
- choose random k=9
- confirm gcd(10,9)=1
- compute
- a = gk(mod p) = 29(mod 11) = 6
- solve
- M = x.a+k.b(mod p-1)
- 5 = 8.6+9.b(mod 10)
- giving b = 3
- signature is (a=6,b=3)
- to verify the signature, confirm the following are correct:
- ya.ab(mod p) = gM(mod p)
- 36.63(mod 11) = 25(mod 11)
DSA (Digital Signature Algorithm)
- DSA was designed by NIST & NSA and is the US federal standard
signature scheme (used with SHA hash alg)
- DSA is the algorithm, DSS is the standard
- there was considerable reaction to its announcement!
- debate over whether RSA should have been used
- debate over the provision of a signature only alg
- DSA is a variant on the ElGamal and Schnorr algorithms
- description of DSA
- p = 2L a prime number, where L= 512 to 1024
bits and is a multiple of 64
- q a 160 bit prime factor of p-1
- g = h(p-1)/q where h is any number less than p-1
with h(p-1)/q(mod p)> 1
- x a number less than q
- y = gx(mod p)
- to sign a message M
- generate random k, k<q
- compute
- r = (gk(mod p))(mod q)
- s = k-1.SHA(M)+ x.r (mod q)
- the signature is (r,s)
- to verify a signature:
- w = s-1(mod q)
- u1= (SHA(M).w)(mod q)
- u2= r.w(mod q)
- v = (gu1.yu2(mod p))(mod q)
- if v=r then the signature is verified
- comments on DSA
- was originally a suggestion to use a common modulus, this would make a
tempting target, discouraged
- it is possible to do both ElGamal and RSA encryption using DSA routines,
this was probably not intended :-)
- DSA is patented with royalty free use, but this patent has been contested,
situation unclear
- Gus Simmons has found a subliminal channel in DSA, could be used to leak
the private key from a library - make sure you trust your library implementer
Other Signature Schemes
Fiat-Shamir
- originally a signature scheme, subsequently modified into a zero knowledge
proof of identity scheme
- based on difficulty of finding square roots mod pq
- this algorithm is patented
Schnorr
- combines ideas from ElGamal and Fiat-Shamir schemes
- uses exponentiation mod p and mod q
- much of the computation can be completed in a pre-computation phase before
signing
- for the same level of security, signatures are significantly smaller than
with RSA
- this algorithm is patented
Key Management
- all cryptographic systems have the problem of how to securely and reliably
distribute the keys used
- in many cases, failures in a secure system are due not to breaking the
algorithm, but to breaking the key distribution scheme
- ideally the distribution protocol should be formally verified, recent
advances make this more achievable
- possible key distribution techniques include:
- physical delivery by secure courier
- eg code-books used submarines
- one-time pads used by diplomatic missions
- registration name and password for computers
- authentication key server (private key, eg Kerberos)
- have an on-line server trusted by all clients
- server has a unique secret key shared with each client
- server negotiates keys on behalf of clients
- public notary (public key, eg SPX)
- have an off-line server trusted by all clients
- server has a well known public key
- server signs public key certificates for each client
Authentication Protocols
- if using a key server, must use some protocol between user and server [4]
- this protocol should be validated, formal techniques exist to acheive this
(Ban logic provers [5])
Challenge-Response
- basic technique used to ensure a password is never sent in the clear
- given a client and a server share a key
- server sends a random challenge vector
- client encrypts it with private key and returns this
- server verifies response with copy of private key
- can repeat protocol in other direction to authenticate server to client
(2-way authentication)
- in simplest form, keys are physically distributed before secure
comminications is required
- in more complex forms, keys are stored in a central trusted key server
Needham-Schroeder
- original third-party key distribution protocol
R M Needham, M D Schroeder, "Using Encryption for Authentication in Large
Networks of Computers", CACM, 21(12), Dec 1978, pp993-998
- given Alice want to communicate with Bob, and have a Key Server S,
protocol is:
Message 1 A -> S A, B, Na
Message 2 S -> A EKas{Na , B, Kab,
EKbs{Kab, A} }
Message 3 A -> B EKbs{Kab, A}
Message 4 B -> A EKab{Nb}
Message 5 A-> B EKab{Nb-1}
nb: Na is a random value chosen by Alice, Nb random
chosen by Bob
- after this protocol runs, Alice and Bob share a secret session key
Kab for secure communication
- unfortunately this protocol includes a fatal flaw - Message3 can be
subject to a replay attack with an old compromised session key by an active
attacker
- this has been corrected either by:
- including a timestamp in messages 1 to 3, which requires synchronised
clocks (by Denning & Sacco 81)
- having A ask B for a random value Jb to be sent to S for return in
EKbs{Kab, A, Jb} (by Needham & Schroeder 87)
- many other protocols exist but care is needed
Kerberos - An Example of a Key Server
- trusted key server system developed by MIT
- provides centralised third-party authentication in a distributed network
- access control may be provided for
- each computing resource
- in either a local or remote network (realm)
- has a Key Distribution Centre (KDC), containing a database of:
- principles (customers and services)
- encryption keys
- basic third-party authentication scheme
- KDC provides non-corruptible authentication credentials (tickets or tokens)
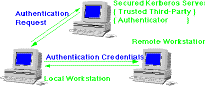
Kerberos - Initial User Authentication
- user requests an initial ticket from KDC
- used as basis for all remote access requests

Kerberos - Request for a Remote Service
- user requests access to a remote service
- obtains a ticket from KDC protected with remote key
- sends ticket with request to remote server

Kerberos - in practise
- currently have two Kerberos versions
- 4 : restricted to a single realm
- 5 : allows inter-realm authentication, in beta test
- Kerberos v5 is an Internet standard
- specified in RFC1510, and used by many utilities
- to use Kerberos
- need to have a KDC on your network
- need to have Kerberised applications running on all participating systems
- major problem - US export restrictions
- Kerberos cannot be directly distributed outside the US in source format
(& binary versions must obscure crypto routine entry points and have no
encryption)
- else crypto libraries must be reimplemented locally
X.509 - Directory Authentication Service
- part of CCITT X.500 directory services
- defines framework for authentication services
- directory may store public-key certificates
- uses public-key cryptography and digital signatures
- algorithms not standardised but RSA is recommended
X.509 Certificate
- issued by a Certification Authority (CA)
- each certificate contains:
- version
- serial number (unique within CA)
- algorithm identifier (used to sign certificate)
- issuer (CA)
- period of validity (from - to dates)
- subject (name of owner)
- public-key (algorithm, parameters, key)
- signature (of hash of all fields in certificate)
- any user with access to CA can get any certificate from it
- only the CA can modify a certificate
CA Hierarchy
- CA form a hierarchy
- each CA has certificates for clients and parent
- each client trusts parents certificates
- enable verification of any certificate from one CA by users of all other
CAs in hierarchy
- X<<A>> means certificate for A signed by authority X
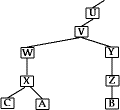
- A acquires B certificate following chain:
-
X<<W>>W<<V>>V<<Y>>Y<<Z>>Z<<B>>
- B acquires A certificate following chain:
-
Z<<Y>>Y<<V>>V<<W>>W<<X>>X<<A>>
Authentication Procedures
- X.509 includes three alternative authentication procedures
One-Way Authentication
- 1 message ( A->B) to establish
- identity of A and that messages is from A
- message intended for B
- integrity & originality of message
Two-Way Authentication
- 2 messages (A->B, B->A) which also establishes
- identity of B and that replay is from B
- reply intended for A
- integrity & originality of reply
Three-Way Authentication
- 3 messages (A->B, B->A, A->B) which enables
- above authentication without syncronised clocks
Security in Practise - Secure Email
- email is one of the most widely used and regarded network services
- currently message contents are not secure
- may be inspected either in transit
- or by suitably priviledged users on destination system
- Email Privacy Enhancement Services
- confidentiality (protection from disclosure)
- authentication (of originator)
- message integrity (protection from modification)
- non-repudiation of origin
- (protection from denial by sender)
- can't assume real-time access to a trusted key server
- often implement using Email Encapsulation
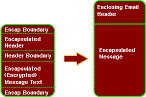
PEM
- Privacy Enhanced Mail
- Internet standard for security enhancements to Internet (RFC822) email
- developed by a Working group of the IETF
- specified in RFC1421, RFC1422, RFC1423, RFC1424
- uses message encapsulation to add features
- confidentiality - DES encryption in CBC mode
- integrity - DES encrypted MIC (MD2/MD5)
- authentication - DES/RSA encrypted MIC
- non-repudiation - RSA encrypted MIC
PEM - Key Management
- central key server (private-key)
- requires access to on-line server
- public-key certificates
- uses X.509 Directory Service Strong Authentication to protect key
certificates
- signed by a Certification Authority (CA)
- CAs form a hierarchy to permit cross-validation of certificates
- CAs must be licenced by RSA Data Inc.
- currently only licenced in US/Canada
PGP
- Pretty Good Privacy
- widely used de facto secure email standard
- developed by Phil Zimmermann
- available on Unix, PC, Macintosh and Amiga systems
- free!!!!
- confidentiality - IDEA encryption
- integrity - RSA encrypted MIC (MD5)
- authentication & non-repudiation - RSA encrypted MIC
- uses grass-roots key distribution
- trusted introducers used to validate keys
- no certification authority hierarchy needed
PGP - In Use
- all PGP functions are performed by a single program
- must be integrated into existing email/news
- each user has a keyring of known keys
- containing their own public and private keys (protected by a password)
- public keys given to you directly by a person
- public keys signed by trusted introducers
- used to sign/encrypt your messages
- used to validate messages received
Sample PGP Message
-----BEGIN PGP SIGNED MESSAGE-----
May all your signals trap
May your references be bounded
All memory aligned
Floats to ints be rounded
Lawrie
-----BEGIN PGP SIGNATURE-----
Version: 2.3
iQBzAgUBLdl1RILpoub8ek7fAQF2nwLuJwVPh8iiFrksXSCe6z37ZdV37pXvsYyz0WAnCBCdpu55yId5/kVhmvusTo10zUHPssPwB99TQq9YsduSfkVeILjfJNJEuUWQkJl8dWvaB+IIEEodF0Xpbc23krnuOA==
=hn90
-----END PGP SIGNATURE-----
PGP - Issues
- were questions of legality, but PGP may now be legally used by anyone in
the world:
- noncommercial use in US/Canada with licenced MIT version
- commercial use in US/Canada with Viacrypt version
- noncommercial use outside the US is probably legal with (non US sourced)
international version
- commercial use outside the US requires an IDEA licence for the
international version
- is on-going legal battle in US over its original export between US govt
and Phil Zimmermann
Security in Practise - SNMP
- SNMP is a widely used network management protocol
- comprises
- management station
- management agent with
- its management information base (MIB)
- linked by network management protocol (GET,SET)
- SNMP v1 lacks any security (GET and SET open if there)
- SNMP v2 includes security extensions for
- message authentication (keyed MD5)
- message secrecy (DES)
- based on the SNMPv2 party (sender & receiver roles)
- used for access control & key management
- all associated information stored in a party MIB
- assumes syncronised clocks (within a set interval)
User Authentication
(ref Davies Ch 7)
- user authentication (identity verification)
- convince system of your identity
- before it can act on your behalf
- sometimes also require that the computer verify its identity with the user
- user authentication is based on three methods
- what you know
- what you have
- what you are
- all then involve some validation of information supplied against a table
of possible values based on users claimed identity

What you Know
Passwords or Pass-phrases
- prompt user for a login name and password
- verify identity by checking that password is correct
- on some (older) systems, password was stored in the clear (this is now
regarded as insecure, since breakin compromises all users of the system)
- more often use a one-way function, whose output cannot easily be used to
find the input value
- either takes a fixed sized input (eg 8 chars)
- or based on a hash function to accept a variable sized input to create the
value
- important that passwords are selected with care to reduce risk of
exhaustive search
Denning Computer (In)security Fig 2 & 3, pp111-12
One-shot Passwords
- one problem with traditional passwords is caused by eavesdropping theit
transfer over an insecure network
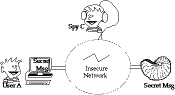
- one possible solution is to use one-shot (one-time) passwords
- these are passwords used once only
- future values cannot be predicted from older values
either generate a printed list, and keep matching list on system to be
accessed (cf home banking)
or use an algorithm based on a one-way function f (eg MD5)
to generate previous values in series (eg SKey)
- start with a secret password s, and number N
- next password in series is
- must reset password after N uses
generally good only for infrequent access
What you Have
- here verify identity based on possession of some object, often also
combined with a password
Magnetic Card, Magnetic Key
- possess item with required code value encoded in it (eg access control
cards)
Smart Card or Calculator
- may interact with system
- may require information from user
- could be used to actively calculate:
- a time dependent password
- a one-shot password
- a challenge-response verification
- public-key based verification
Davies fig 7.7 & 7.8 pp184-84
What you Are
- here verify identity based on your physical characteristics or involuntary
reponse patterns
- known as biometrics
- characteristics used include:
- signature (usually dynamic)
- fingerprint
- hand geometry
- face or body profile
- speech
- retina pattern
- always have tradeoff between
- false rejection (type I error)
- false acceptance (type II error)
Davis fig 7.12 p195
[1] see Schneier p322
[2] follow with Schneier pp330-332
[3] follow with Schneier pp334-335
[4] see Dieter Gollman, Thomas Beth, Frank Damm,
"Authentication Services in Distributed Systems", Computers & Security,
12(8), 1993, pp753-764
[5] see Anish Mathuria, "Automating Ban Logic", MSci(Hons),
University of Wollongong, 1993
[CSC Info]
Lawrie.Brown@adfa.oz.au / 22-May-96








